DM

TD 3ème partie

Intégration

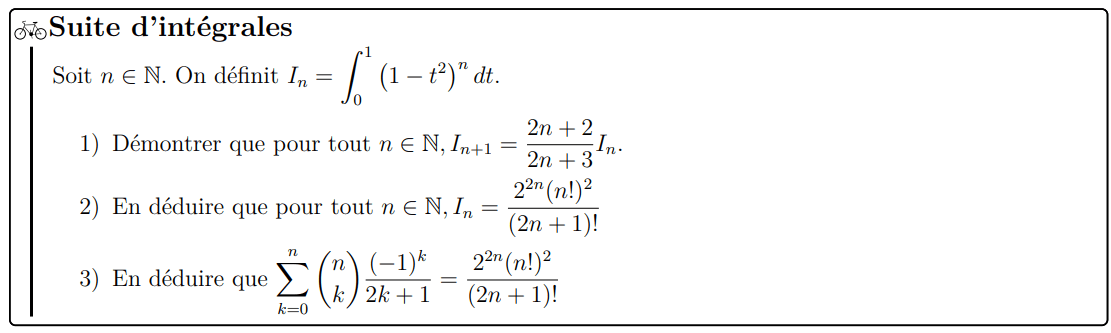
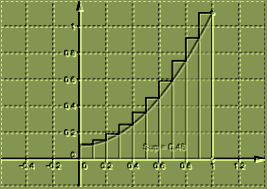
1°) Soit \(n\in\N\). On procède par intégration par parties:

\int_0^1 (1-t^2)^{n+1}dt = \int_0^1 u'(t)v(t)dt

\text{où} \\ u:t\mapsto t \text{ et } v: t\mapsto (1-t^2)^{n+1} \text{ sont de classe }\mathcal{C}^1 sur [0,1]\\ u':t\mapsto 1 \text{ et } v': t\mapsto -2(n+1)t(1-t^2)^n

=\left[u(t)v(t)\right]_0^1 - \int_0^1 u(t)v'(t)dt

\int_0^1 (1-t^2)^{n+1}dt =\left[t (1-t^2)^{n+1}\right]_0^1 +2(n+1)\int_0^1 t^2 (1-t^2)^n dt

Donc

\int_0^1 (1-t^2)^{n+1}dt =\left[t (1-t^2)^{n+1}\right]_0^1 +2(n+1)\int_0^1 t^2 (1-t^2)^n dt

=2(n+1)\int_0^1 t^2 (1-t^2)^n dt

=2(n+1)\int_0^1 (t^2-1+1) (1-t^2)^n dt

I_{n+1} =-2(n+1)\int_0^1 (1-t^2)^{n+1} dt+2(n+1)\int_0^1 (1-t^2)^{n+1} dt

Ainsi,

I_{n+1} =-2(n+1) I_{n+1}+2(n+1)I_n

\iff I_{n+1} +2(n+1) I_{n+1}=2(n+1)I_n

\iff(2n+3) I_{n+1} =2(n+1)I_n

\iff I_{n+1} =\frac{2n+2}{2n+3}I_n

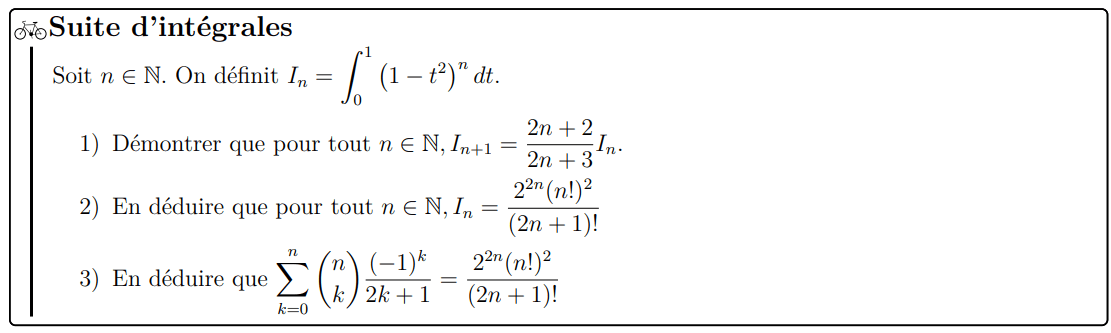
2°) Stricte positivité de \(I_n\)
\(\forall t\in [0,1], 1-t^2=(1-t)(1+t) \geqslant 0\)

Donc pour tout \(n\in\N\), \(t\mapsto (1-t^2)^n \) est positive sur [0;1]
et par conséquent \(I_n \geqslant 0\)

Si \(I_n=0\) alors \(t\mapsto (1-t^2)^n \) est nulle sur [0;1]
D'après la propriété:
Si \(f\geqslant 0\) sur [a,b] et \(\int_{[a,b]}f=0 \)alors \(f=0\) sur [a,b] )
Ce qui est absurde. On déduit que \(I_n>0\)

Pour \(n=0:\)

On procède par récurrence sur \(\N\) :

\(\underline{Initialisation}\):

\text{D'une part:}\\ I_0=\int_0^1 1 dt=1

\text{D'autre part:}\\ \frac{2^{2 n}(n!)^2}{(2 n+1)!}= \frac{2^{0}(0!)^2}{1!}=1

\mathcal{P}(0) \text{est vraie}

\text{Soit } \mathcal{P}(n) \text{ la proposition définie par :}

\mathcal{P}(n) :\left( I_n= \frac{2^{2 n}(n!)^2}{(2 n+1)!} \right)

\(\underline{Hérédité}\):

\text{Soit } n\in \N, \text{montrons que }(\mathcal{P}(n)\Rightarrow \mathcal{P}(n+1))

\mathcal{P}(n)

\Rightarrow \left( I_n= \frac{2^{2 n}(n!)^2}{(2 n+1)!} \right)

\Rightarrow \left( I_{n+1} = \frac{2n+2}{2n+3}I_n =\frac{2n+2}{2n+3} \frac{2^{2 n}(n!)^2}{(2 n+1)!} \right)

\Rightarrow \left( I_{n+1} =\frac{(2n+2)(2n+2)}{(2n+3)(2n+2)} \frac{2^{2 n}(n!)^2}{(2 n+1)!} \right)

\Rightarrow \left( I_{n+1} = 4 (n+1)(n+1) \frac{2^{2 n}(n!)^2}{(2 n+3)!} = \frac{2^{2 (n+1)}((n+1)!)^2}{(2 (n+1)+1)!} \right)

\Rightarrow \mathcal{P}(n+1)

\(\underline{Conclusion}\): Pour tout \(n\in\N\), \( I_n= \dfrac{2^{2 n}(n!)^2}{(2 n+1)!}\)

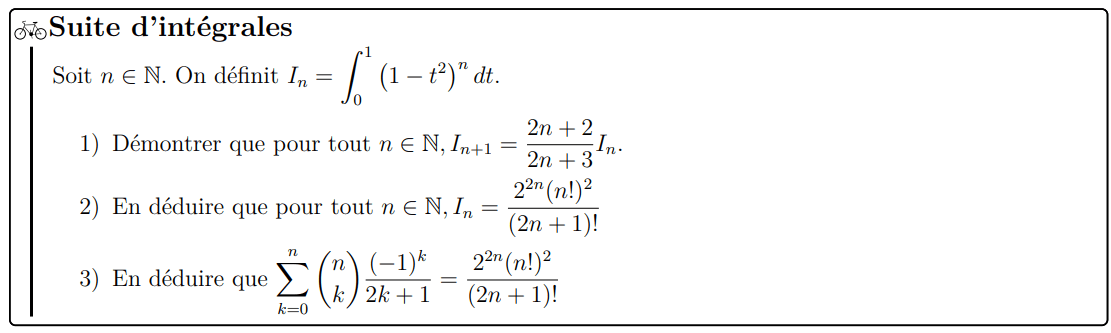
3°) On utilise la formule du binôme de Newton:

(1-t^2)^n=(-t^2+1)^n=\sum_{k=0}^n \binom{n}{k} (-t^2)^k =\sum_{k=0}^n \binom{n}{k} (-1)^k t^{2k}

Donc, d'une part,

I_n=\int_0^1 (1-t^2)^n dt =\int_0^1 \sum_{k=0}^n \binom{n}{k} (-1)^k t^{2k} dt =\sum_{k=0}^n \binom{n}{k} (-1)^k \int_0^1 t^{2k} dt

I_n= \sum_{k=0}^n \binom{n}{k} (-1)^k \left[ \frac{1}{2k+1} t^{2k+1} \right]_0^1 =\sum_{k=0}^n \binom{n}{k} (-1)^k \frac{1}{2k+1} (*)

D'autre part,

\( I_n= \dfrac{2^{2 n}(n!)^2}{(2 n+1)!}\) (**)

(*) et (**) permettent de conclure

1°) Si \(f\) est paire

\(\forall x\in \R\),

\( F(x)=\int_0^x f(t) dt \)

Donc, \( F(-x)=\displaystyle\int_0^{-x} f(t) dt \)

On effectue le changement de variable affine suivant :

\(y=-t\) ainsi \(dy=-dt\)

\( F(-x)=\displaystyle\int_0^{x} -f(-y) dy \)

\( F(-x)=\displaystyle\int_0^{x} -f(y) dy =-F(x) \)

F est impaire

erratum : et que F(0)=0

1°) Si \(F\) est impaire

\(\forall x\in \R\),

\( F(-x)=-F(x) \)

Donc, par dérivation :
\( - F'(-x)=-F'(x) \iff -f(-x)=-f(x) \iff f(-x)=f(x) \)

alors \(f\) est paire

La réciproque est vraie

erratum : et que F(0)=0

et \( F(-0)=-F(0) \) qui implique: \(F(0)=0 \)

2°) Si \(f\) est impaire

\(\forall x\in \R\),

\( F(x)=\int_0^x f(t) dt +F(0)\)

Donc, \( F(-x)=\displaystyle\int_0^{-x} f(t) dt +F(0)\)

On effectue le changement de variable affine suivant :

\(y=-t\) ainsi \(dy=-dt\)

\( F(-x)=\displaystyle\int_0^{x} -f(-y) dy +F(0)\)

\( F(-x)=\displaystyle\int_0^{x} f(y) dy +F(0) =F(x) \)

erratum : et que F(0)=0

F est paire

2°) Si \(F\) est paire

\(\forall x\in \R\),

\( F(-x)=F(x) \)

Donc, par dérivation :
\( - F'(-x)=F'(x) \iff -f(-x)=f(x) \iff f(-x)=-f(x) \)

alors \(f\) est impaire

La réciproque est vraie

erratum : et que F(0)=0

1°)

Soit \(f:t\mapsto \dfrac{1}{\sqrt{1+t^2+t^4}} \)

\text{Soient } f_1 :\left\{\begin{array}{ccc} \R & \to& [1;+\infty[ \\ t & \mapsto & 1+t^2+t^4 \end{array}\right.

f_2 :\left\{\begin{array}{ccc} [1;+\infty[ & \to& [1;+\infty[ \\ t & \mapsto & \sqrt{t} \end{array}\right.

f_3 :\left\{\begin{array}{ccc} [1;+\infty[ & \to& ]0;1] \\ t & \mapsto & \dfrac{1}{t} \end{array}\right.

f_1,f_2 \text{ et } f_3 \text{ sont continues}

\text{Donc } f= f_3 \circ f_2 \circ f_1 \text{ est continue sur } \R\\ \text{ et admet donc une primitive } F \text{ définie et dérivable sur } \R

1°)

Soit \(f:t\mapsto \dfrac{1}{\sqrt{1+t^2+t^4}} \)

\text{Soient } f_1 :\left\{\begin{array}{ccc} \R & \to& [1;+\infty[ \\ t & \mapsto & 1+t^2+t^4 \end{array}\right.

f_2 :\left\{\begin{array}{ccc} [1;+\infty[ & \to& [1;+\infty[ \\ t & \mapsto & \sqrt{t} \end{array}\right.

f_3 :\left\{\begin{array}{ccc} [1;+\infty[ & \to& ]0;1] \\ t & \mapsto & \dfrac{1}{t} \end{array}\right.

f_1,f_2 \text{ et } f_3 \text{ sont continues.}

\text{Donc } f= f_3 \circ f_2 \circ f_1 \text{ est continue sur } \R\\ \text{ et admet donc une primitive } F \text{ définie et dérivable sur } \R \\ \text{telle que } F(0)=0

\forall x\in \R , g(x)=F(2x)-F(x)

g \text{ est la somme de 2 fonctions dérivables sur } \R

g \text{ est donc dérivable sur } \R

\text{Et, } g'(x)=2F'(2x)-F'(x)=2f(2x)-f(x)

g' \text{ est la somme de 2 fonctions continues sur } \R

g \text{ est donc de classe } \mathcal{C}^1 \text{ sur }\R

1°)

\forall x\in \R, g'(x)=2F'(2x)-F'(x)=2f(2x)-f(x)

\forall x\in \R, g'(x)=\dfrac{2}{\sqrt{1+4x^2+16x^4}}-\dfrac{1}{\sqrt{1+x^2+x^4}}

3°)

\forall x\in \R_+, g'(x)=\dfrac{2\sqrt{1+x^2+x^4}-\sqrt{1+4x^2+16x^4}}{\sqrt{1+4x^2+16x^4} \sqrt{1+x^2+x^4}}

g'(x) \text{ est du même signe que : } \\ 2\sqrt{1+x^2+x^4}-\sqrt{1+4x^2+16x^4}\\ =\sqrt{4+4x^2+4x^4}-\sqrt{1+4x^2+16x^4}

\forall x\in \R_+,

2°)

\(f\) est paire et \(F(0)=0\) donc \(F\) est impaire

\forall x\in \R, g(-x)=F(-2x)-F(-x)=-F(2x)+F(x)=-g(x)

\(g\) est impaire

Etude de signe de la dérivée:

\text{ Outil: } \\ \forall (a,b)\in (\R_+^*)^2, \\ \sqrt{a}-\sqrt{b}=\frac{a-b}{\sqrt{a}+\sqrt{b}}

g'(x) \text{ est du même signe que : } \\ =\sqrt{4+4x^2+4x^4}-\sqrt{1+4x^2+16x^4}

\forall x\in \R_+,

g'(x) \text{ est du même signe que : } \\ (4+4x^2+4x^4)-(1+4x^2+16x^4) =3-12x^4\\ =3(1-4x^4) =3(1-2x^2)(1+2x^2) =3(1-x\sqrt{2})(1+x\sqrt{2}) (1+2x^2)

\forall x\in\R_+, g'(x) \text{ est du même signe que : } (1-x\sqrt{2})

\forall x\in\R_+, g'(x) \text{ est } \left\{ \begin{array}{ccc} \text{ positif }&\text{ Si }& 0\leqslant x \leqslant \frac{1}{\sqrt{2}}\\ \text{ négatif }&\text{ Si }& x\geqslant \frac{1}{\sqrt{2}} \end{array} \right.

g \text{ est } \left\{ \begin{array}{ccc} \text{ croissante }&\text{ Sur }& [ 0;\frac{1}{\sqrt{2}}]\\\\ \text{ décroissante }&\text{ Sur }& [\frac{1}{\sqrt{2}};+\infty[ \end{array} \right.

4°)

Rappels: (Cours DL)

Existence de DL :

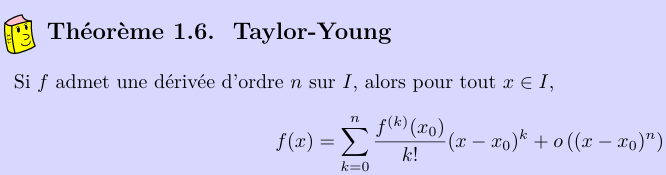
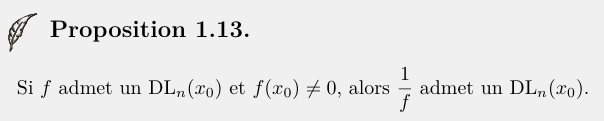
Existence de DL d'inverse:

Conditions suffisantes

Existence de DL d'une primitive :

\text{Donc par composition , } \varphi : x\mapsto \sqrt{1+x^2+x^4} \text{ est indéfiniment dérivable sur }\R

\text{Soient } f_1 :\left\{\begin{array}{ccc} \R & \to& [1;+\infty[ \\ t & \mapsto & 1+t^2+t^4 \end{array}\right.

f_2 :\left\{\begin{array}{ccc} [1;+\infty[ & \to& [1;+\infty[ \\ t & \mapsto & \sqrt{t} \end{array}\right.

f_1 \text{ et } f_2 \text{ sont indéfiniement dérivables sur leur ensemble de définition}

Pour tout \(n\in\N\) \(\varphi\) admet un \(DL_n(0) \)
D'après le théorème de Taylor Young

\(\varphi(0)=1\neq 0\) admet \(\dfrac{1}{\varphi}\) un \(DL_n(0) \)

\(F\) admet donc un \( DL_{n+1}(0)\) et un \( DL_{0}(0)\) (car F est continue en 0)

\text{On pose : } u= x^2+x^4\\ \text{Lorsque } x\to 0 , u\to 0\\\\

\sqrt{1+x^2+x^4}= (1+u)^\frac{1}{2}\underset{0}{=} 1+\frac{1}{2}u-\frac{1}{8}u^2 +o(u^2)

\sqrt{1+x^2+x^4}\underset{0}{=} 1+\frac{1}{2}(x^2+x^4)-\frac{1}{8}(x^2+x^4)^2 +o((x^2+x^4)^2)

\sqrt{1+x^2+x^4}\underset{0}{=} 1+\frac{1}{2}(x^2+x^4)-\frac{1}{8}x^4 +o(x^4)

\sqrt{1+x^2+x^4}\underset{0}{=} 1+\frac{1}{2}x^2+\frac{3}{8}x^4 +o(x^4)

f(x)=\frac{1}{ \sqrt{1+x^2+x^4}} \underset{0}{=} 1-\frac{1}{2}x^2-\frac{1}{8}x^4 +o(x^4)

F(x) \underset{0}{=} F(0)+ x-\frac{1}{6}x^3-\frac{1}{40}x^5 +o(x^5)

g(x)=F(2x)-F(x) \underset{0}{=} F(0)+ 2x-\frac{1}{6}8x^3-\frac{1}{40}32x^5 +o(x^5) -\left( F(0)+ x-\frac{1}{6}x^3-\frac{1}{40}x^5 \right)

g(x)\underset{0}{=} x-\frac{7}{6}x^3-\frac{31}{40}x^5 +o(x^5)