Décomposition en éléments simples de Fractions rationnelles
14/04/2025
TD
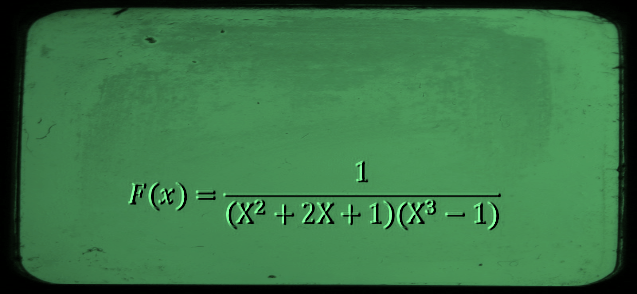


Tous les pôles sont simples
Multiplication par \(X-3\):
Multiplication par \(X+2\):
Multiplication par \(X\):
Avec l' affectation \(X=3\):
Avec l' affectation \(X=-2\):
Avec l' affectation \(X=0\):

\( \alpha \) est un pôle donc
- D'après les formules de Taylor
Sinon \( \alpha \) est plus un pôle multiple

- Multiplication par \(X-\alpha\) membre à membre :
- On fait X tendre vers \(\alpha\) membre à membre :

- Les pôles sont simples et correspondent aux racines n-ième de 1:

La décomposition en éléments simples de F est :
Multiplication par \((X-1)^2\):
puis affectation \(X=1\):
Calcul de \( \lambda_1\) et \( \lambda_2\) pour les éléments simples associés au pôle 1
avec G défini en 1
Réduction de la multiplicité:
Multiplication par \((X-1)\) Avec l' affectation \(X=1\):

La décomposition en éléments simples de F est :
Calcul de \( \lambda_3\) et \( \lambda_4\) pour les éléments simples associés au pôle -1
MAiS NON
On pourrait faire comme pour \( \lambda_1\) et \( \lambda_2\)
Car on peut observer que \( F\) est paire \( F(X)=F(-X) \)

$$A= 1$$
$$B= (X-1)^3=X^3-3X^2+3X-1$$
- On pose:
- Donc on peut effectuer une division suivant les puissances croissantes de A par B à l'ordre 3. Obtient le quotient
$$Q_1=-1-3X-6X^2-10X^3$$
- On en déduit les éléments simples liés au pôle 0

$$A= 1$$
$$B= (Y+1)^3=Y^3+3Y^2+3Y+1$$
- Changement de variable Y=X-1
- Donc on peut effectuer une division suivant les puissances croissantes de A par à l'ordre 3. On obtient le quotient :
$$Q_2=X^3+3X^2+3X+1$$
$$P=(X+1)^3$$
$$P'=3X^2+6X+3$$
$$P'=3(X^2+2X+1)=3(X+1)^2$$
$$P=X^3+3X^2+3X+1$$
sans surprise !!
Autre exemple de DES à faire pour jeudi:

Méthode:
- On enchaîne des divisions euclidiennes de numérateurs\( N_i\) par P où \(P=X^2+X+1\)
- Ainsi
- On répète le procédé
- etc... Jusqu'à n'avoir que des éléments simples
- Ainsi

- On multiple membre à membre par X puis on remplace X par 0
- On réduit la multiplicité du pôle 0
sera de la forme
Et on poursuit la décomposition de comme dans l'exercice 7
avec P irréductible et deg(P)=2