Décomposition en éléments simples de Fractions rationnelles

\mathbb{K}(X)

\mathbb{K} \text{=} \mathbb{R} \text{ ou } \mathbb{C}

10/04/2025

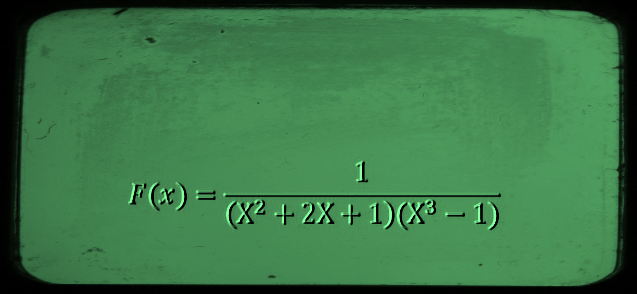
\mathbb{K}(X)= \left\lbrace \dfrac{P}{Q} , (P,Q)\in \mathbb{K}[X]^2 , Q\neq 0 \right\rbrace

\(\mathbb{K}(X) \) désigne l'ensemble des fractions rationnelles

1.1

Exemples :

\( F=\dfrac{X^-4X+3X^2+X1}{5X^3-1} \in \mathbb{R}(X) \)

\( F=\dfrac{1+7i}{2(X+1)(X-i)(X^2+1)} \in \mathbb{C}(X) \)

\text{Soit} (A,B)\in \mathbb{K}[X]^2 , B\neq 0

Division euclidienne dans \( \mathbb{K} [X] \) (vu en algèbre)

2.1

\exists ! (Q,R)\in \mathbb{K}[X]^2 , A=BQ+R ,\deg(R) < \deg(B)

\(A\)

\(B\)

\(Q\)

\(R\)

\(BQ\)

dividende

diviseur

quotient

reste

Théorème:

X^2+1

X^2-1

\( X^4 -2X+3\)

\( X^4+X^2\)

\( -X^2 -2X+3\)

\( -X^2 -1\)

\( -2X +4\)

X^4-2X+3=(X^2+1)(X^2-1)+(-2X+4)

Effectuer la division euclidienne de \(X^4-2X+3\) par \(X^2+1\)

Entrainez -vous ici

Exemple :

Exercice :

Fraction rationnelle irréductible

3.1

\text{Soit } F=\dfrac{A}{B} \in \mathbb{K}(X)

Définition:

\text{Rendre irréductible} \dfrac{A}{B}= \dfrac{X^2+2X-3}{X^4-2X^2+1}

Dans ce chapitre, on rendra une fraction irréductible à partir de décomposition du dénominateur en produit de facteurs irréductibles

PGCD(A,B)\overset{notation}{=}A\wedge B =1

\( F\) est irreductible lorsque :

On dit que \( A\) et \( B\) sont premiers entre eux

Méthode:

Exemple :

X^4-2X^2+1 =(X^2-1)^2 =\left( (X-1) (X+1)\right)^2 =(X-1)^2 (X+1)^2

\( B(1) =0 \) et \( A(1) =0 \)

\text{On a : } \dfrac{A}{B}= \dfrac{(X-1)(X+3)}{(X-1)^2 (X+1)^2}= \dfrac{X+3}{=(X-1) (X+1)^2}

\text{Soit } F \in \mathbb{K}(X)

Partie entière d'une fraction rationnelle

4.1

\exists ! (E,N)\in \mathbb{K}[X]^2 , F=E+ \dfrac{N}{D} ,\deg(N) < \deg(D)

Théorème:

\( E\) est la partie entière de \( F\)

\( \dfrac{N}{D}\) est la partie fractionnaire de \( F\)

Soit \(F=\dfrac{A}{D}\in \mathbb{K}[X]\) .
On effectue la division euclidienne de A par D:
\(A=DE+N \)
\(E\) est le quotient et \(N \) est le reste. \( \deg(N) <\deg(B) \)
Ainsi: \(F=\dfrac{A}{D}=E+\dfrac{N}{D} \) .

Preuve :

Méthode :

Déterminer la partie entière de \(\dfrac{A}{D} \)

C' est déterminer le quotient de la division euclienne de \(A \) par \(D \).

Preuve :

D=\prod_{k=1}^n P_k^{m_k} = P_1^{m_1} \times P_2^{m_2} \times \cdots \times P_n^{m_n}

Soit \(F\) une fraction rationnelle irréductible.
\(F =\dfrac{N}{D}\)

telle que \(D\) admet pour décomposition
en facteurs irréductibles dans \(\mathbb{K}[X]\)

\(F\) s'écrit de façon unique sous la forme:

F = E + \Big( \frac{Q_{1,1}}{P_1} + \frac{Q_{1,2}}{P^2_1}+ \cdots + \frac{Q_{1,m_1}}{P^{m_1}_1} \Big) + \cdots + \Big( \frac{Q_{n,1}}{P_n} + \frac{Q_{n,2}}{P^2_n}+ \cdots + \frac{Q_{n,m_n}}{P^{m_n}_n} \Big)

5.1

Théorème:

Décomposition d'une fraction rationnelle
en éléments simples dans \(\mathbb{K}(X)\)

avec \( \deg(Q_{i,j})<\deg(P_i)\)

Text

Eléments simples

5.2

Preuve de Fréderic MILLET avec \(\mathbb{K}= \mathbb{C}\)

Décomposition d'une fraction rationnelle
en éléments simples dans \(\mathbb{K}(X)\)

Le dénominateur est de la forme :

6.1

Les éléments simples de \(\dfrac{N}{D}\)
avec \(\deg(N)<\deg(D)\)

Cas où \(\mathbb{K} \)= \(\mathbb{C} \)

D=a\prod_{k=1}^n (X-\alpha_i) ^{m_k} = a (X-\alpha_1)^{m_1} \cdots (X-\alpha_n)^{m_n}

\dfrac{N}{D}=

les \( (\lambda_{i,j})\) sont dans \(\mathbb{C} \)

\dfrac{\lambda_{1,m_1}}{(X-\alpha_{1})^{m_1} } +\dfrac{\lambda_{1,m_1-1}}{(X-\alpha_{1})^{m_1-1} }+ \cdots+\dfrac{\lambda_{1,1}}{(X-\alpha_{1})^{1} }

+ \qquad\cdots

+ \dfrac{\lambda_{n,m_n}}{(X-\alpha_{n})^{m_n} } +\dfrac{\lambda_{n,m_n-1}}{(X-\alpha_{n})^{m_n-1} }+ \cdots+\dfrac{\lambda_{n,1}}{(X-\alpha_{n})^{1} }

Le dénominateur est de la forme :

6.2

Les éléments simples de \(\dfrac{N}{D}\)
avec \(\deg(N)<\deg(D)\)

Cas où \(\mathbb{K} \)= \(\mathbb{C} \)

D=a\prod_{k=1}^n (X-\alpha_i) ^{m_k} = a (X-\alpha_1)^{m_1} \cdots (X-\alpha_n)^{m_n}

\dfrac{N}{D}=

\dfrac{\lambda_{1,m_1}}{(X-\alpha_{1})^{m_1} } +\dfrac{\lambda_{1,m_1-1}}{(X-\alpha_{1})^{m_1-1} }+ \cdots+\dfrac{\lambda_{1,1}}{(X-\alpha_{1})^{1} }

+G_1

\text{où } G_1\in \mathbb{C}(X)

\text{et } G_1(\alpha_1) \text{est défini}

\dfrac{N}{D}=

\dfrac{\lambda_{i,m_i}}{(X-\alpha_{i})^{m_i} } +\dfrac{\lambda_{i,m_i-1}}{(X-\alpha_{i})^{m_1-1} }+ \cdots+\dfrac{\lambda_{i,1}}{(X-\alpha_{i})^{1} } +G_i

!!! On a le même résultat pour les autres pôles !!!

\text{où } G_i\in \mathbb{C}(X)

\text{et } G_i(\alpha_i) \text{est défini}

Le dénominateur étant de la forme :

6.3

Les éléments simples de \(\dfrac{N}{D}\)
avec \(\deg(N)<\deg(D)\)

Cas où \(\mathbb{K} \)= \(\mathbb{C} \)

D=a\prod_{k=1}^n (X-\alpha_i) ^{m_k} = a (X-\alpha_1)^{m_1} \cdots (X-\alpha_n)^{m_n}

Pour tout \(i \in \llbracket 1 ,n\rrbracket\), \( \alpha_i \) étant un pôle de multiplicité \(m_i\)

Il y a \(m_i\) éléments simples associés à \( \alpha_i\) :

\dfrac{\lambda_{m_i}}{(X-\alpha_{i})^{m_i} } ,\dfrac{\lambda_{m_i-1}}{(X-\alpha_{i})^{m_i-1} } \cdots\dfrac{\lambda_{1}}{(X-\alpha_{i})^{1} }

Reste à TROUVER les \( (\lambda_k)\)

Méthode 1
Calcul des \( \lambda_k\)

Multiplication par \( (X-\alpha_i)^{m_i} \)
Affectation \(X=\alpha_i \)
Réduction de la multiplicité *

6.4

6.5

Exemple :

\text{Décomposer } F= \dfrac{X^8+2}{X^3(X-1)^2(X+2)} \text{en éléments simples dans } \mathbb{C}[X]

X^8+2

X^6-3X^4+2X^3

-2X^5+9X^4-6X^3+2

X^2+3

X^8-3X^6+2X^5

3X^6-2X^5+2

3X^6-9X^4+6X^3

F= \dfrac{X^8+2}{X^6-3X^4+2X^3}=X^2+3+\dfrac{-2X^5+9X^4-X^3+2}{X^3(X-1)^2(X+2)}

Etape 1 : Rechercher de E la partie entière

6.6

\text{Eléments simples de } F_1=\dfrac{-2X^5+9X^4-6X^3+2}{X^3(X-1)^2(X+2)} \text{dans } \mathbb{C}[X]

Etape 2 : Recherche des élements simples

\text{Les pôles sont: }\\ 0 \text{ de multiplicité } 3 \\ 1 \text{ de multiplicité } 2 \\ -2 \text{ de multiplicité } 1

\text{Eléments simples associés au pôle -2 :}

Multiplication par \(X+2\) et affectation \(X=-2\) :

(X+2)F_1= \dfrac{-2X^5+9X^4-6X^3+2}{X^3(X-1)^2}=\lambda_1 +(X+2)G_1

F_1=\dfrac{\lambda_{1}}{(X+2)^{1} } +G_1 \qquad\text{ où } G(-2) \text{ est défini}

On a:

\lambda_1 =\dfrac{-43}{12}

puis :

\dfrac{-2(-2)^5+9(-2)^4-6(-2)^3+2}{(-2)^3((-2)-1)^2}=\lambda_1

6.7

\text{Eléments simples de } F_1=\dfrac{-2X^5+9X^4-6X^3+2}{X^3(X-1)^2(X+2)} \text{dans } \mathbb{C}[X]

Etape 2 : Recherche des élements simples

\text{Eléments simples associés au pôle 1 :}

Multiplication par \((X-1)^2\) et affectation \(X=1\) :

(X-1)^2F_1= \dfrac{-2X^5+9X^4-6X^3+2}{X^3(X+2)}=\lambda_2 +\lambda_3(X-1) +(X-1)^2 G_2

F_1=\dfrac{\lambda_{2}}{(X-1)^{2} } +\dfrac{\lambda_{3}}{X-1} +G_2 \qquad\text{ où } G_2(1) \text{ est défini}

On a:

puis :

\lambda_2=1

F_1 -\dfrac{1}{(X-1)^{2} } =\dfrac{\lambda_{3}}{X-1} +G_2

Réduction de la multiplicité:

\iff -\dfrac{-2X^5+8X^4-8X^3+2}{X^3(X-1)^2(X+2)} = -\dfrac{-2X^4+6X^3-2X^2-2X-2}{X^3(X-1)(X+2)}=\dfrac{\lambda_{3}}{X-1} +G_2

\lambda_3 =-\dfrac{2}{3}

6.8

\text{Eléments simples de } F_1=\dfrac{-2X^5+9X^4-6X^3+2}{X^3(X-1)^2(X+2)} \text{dans } \mathbb{C}[X]

Etape 2 : Recherche des élements simples

\text{Eléments simples associés au pôle 0 :}

\lambda_4=1

Il faut répéter :

F_1=\dfrac{\lambda_{4}}{X^{3} } +\dfrac{\lambda_{5}}{X^2} +\dfrac{\lambda_{6}}{X}+G_3 \qquad\text{ où } G_3(0) \text{ est défini}

3 Multiplications- affectations -2 Réduction de la multiplicité :

Multiplication par \(X^3\) et affectation \(X=0\) :

Réduction de la multiplicité :

\dfrac{-2X^4+9X^3-7X^2+3}{X^2(X-1)^2(X+2)} = \dfrac{\lambda_{5}}{X^2} +\dfrac{\lambda_{6}}{X}+G_2 \qquad\text{ où } G_2(0) \text{ est défini}

Multiplication par \(X^2\) et affectation \(X=0\) :

\lambda_5=\dfrac{3}{2}

Réduction de la multiplicité :

\dfrac{-2X^3+\frac{15}{2}X^2-7X+\frac{9}{2}} {X(X-1)^2(X+2)} =\dfrac{\lambda_{6}}{X}+G_2 \qquad\text{ où } G_2(0) \text{ est défini}

Multiplication par \(X\) et affectation \(X=0\) :

\lambda_6=\dfrac{9}{4}

Méthode 2
pour les pôles multiples

Changement de variable \(Y=X-\alpha\)
division suivant les puissances croissantes

6.9

6.10

\text{Eléments simples de } F_1=\dfrac{-2X^5+9X^4-6X^3+2}{X^3(X-1)^2(X+2)} \text{dans } \mathbb{C}[X]

Etape 2 : Recherche des élements simples

\text{Eléments simples associés au pôle 0 :}

\text{on pose :} Y=X-0 \text{ changement inutile dans ce cas !}

\text{On effectue la division suivant les puissances croissantes de }\\ 2-6X^3+9X^4-2X^5 \text{ par } 2-3X+X^3

2-6X^3+9X^4-2X^5

2-3X+X^3

1+\dfrac{3}{2}X+\dfrac{9}{4}X^2

2-3X+X^3

3X-7X^3+9X^4-2X^5

3X-\frac{9}{2}X^2+\frac{3}{2}X^4

\frac{9}{2}X^2+\cdots

6.11

\text{Eléments simples de } F_1=\dfrac{-2X^5+9X^4-6X^3+2}{X^3(X-1)^2(X+2)} \text{dans } \mathbb{C}[X]

Etape 2 : Recherche des élements simples

\text{Eléments simples associés au pôle 0 :}

1+\dfrac{3}{2}X+\dfrac{9}{4}X^2

A partir du quotient

F_1=\dfrac{1}{X^{3} } +\dfrac{3}{2X^2} +\dfrac{9}{4X}+G_3 \qquad\text{ où } G_3(0) \text{ est défini}

Le dénominateur est de la forme :

7.1

Les éléments simples de \(\dfrac{N}{D}\)
avec \(\deg(N)<\deg(D)\)

Cas où \(\mathbb{K} \)= \(\mathbb{R} \)

D= a (X-\alpha_1)^{m_1} \cdots (X-\alpha_n)^{m_n} \prod_{i=1}^m (X+p_iX+q_i) ^{l_i}

\text{A chaque facteur } (X^2+p_iX+q_i)^{l_i} \\ \text{est associé } l_i \text{ éléments simples de 2ème espèce}

\dfrac{a_{i,n}X+b_{i,n}} {(X^2+p_iX+q_i)^{l_i}}+\cdots+\dfrac{a_{i,1}X+b_{i,1} }{(X^2+p_iX+q_i)^1}

Tous les coefficients sont réels

PREMIERS
EXEMPLES

F_1=\dfrac{aX+b}{cX+d}

Exemple 1

F_1=\dfrac{a}{c} +\dfrac{\delta}{c(cx+d)}

\text{où } \delta=bc-ad

F_1=\dfrac{a}{c} +\dfrac{\delta}{c(cx+d)}

\text{où } \delta=bc-ad

F_1=\dfrac{ax+b}{cx+d}

F_1=\dfrac{a}{c} +\dfrac{b-\frac{ad}{c}}{cx+d}

ax+b

cx+d

\dfrac{a}{c}

ax+\frac{ad}{c}

b-\frac{ad}{c}

F_2=\dfrac{1}{X^2-X}

Exemple 2

F_2=\dfrac{1}{X^2-X}

F_2=\dfrac{1}{X(X-1)}

\(F_2\) irréductible et partie entière nulle

F_2=\dfrac{a}{X}+\dfrac{b}{X-1}

\Leftrightarrow XF_2 =a+\dfrac{bX}{X-1}\\

Pour \(X=0\), on a: a =- 1

\Leftrightarrow \dfrac{1}{X-1} =a+\dfrac{bX}{X-1}\\

F_2=\dfrac{a}{X}+\dfrac{b}{X-1}

\Leftrightarrow (X-1)F_2 =\dfrac{a(X-1)}{X}+b\\

\Leftrightarrow \dfrac{1}{X} =\dfrac{a(X-1)}{X}+b\\

Pour X=1 , on a: b=1

=-\dfrac{1}{X}+\dfrac{1}{X-1}

F_3=\dfrac{X^2+X+1}{X^4-5X^2+4}

Exemple 3

F_3=\dfrac{X^2+X+1}{X^4-5X^2+4}

=\dfrac{X^2+X+1}{(X-2)(X+2)(X-1)(X+1)}

F_3=\dfrac{a}{X-2}+\dfrac{b}{X+2}+\dfrac{c}{X-1}+\dfrac{d}{X+1}

Multiplication par et affectation :

X-1

X=1

c=-\dfrac{1}{2}

Multiplication par et affectation :

X-2

X=2

a=\dfrac{7}{12}

Multiplication par et affectation :

Multiplication par et affectation :

X+1

X=-1

d=-\dfrac{1}{6}

X+2

X=-2

b=-\dfrac{1}{4}

F_4=\dfrac{X+1}{(X-1)^2X^3}=\dfrac{2}{(X-1)^2}-\dfrac{5}{X-1}+\dfrac{1}{X^3}+\dfrac{3}{X^2}+\dfrac{5}{X}

F_3=\dfrac{a}{X-2}+\dfrac{b}{X+2}+\dfrac{c}{X-1}+\dfrac{d}{X+1}

F_3=\dfrac{7}{12(X-2)}-\dfrac{1}{4(X+2)}-\dfrac{1}{2(X-1)}-\dfrac{1}{6(X+1)}

F_3=\dfrac{X^2+X+1}{X^4-5X^2+4}

F_4=\dfrac{X+1}{(X-1)^2X^3}

Exemple 4

F_4=\dfrac{X+1}{(X-1)^2X^3}=\dfrac{a}{(X-1)^2}+\dfrac{b}{X-1}+\dfrac{c}{X^3}+\dfrac{d}{X^2}+\dfrac{e}{X}

Multiplication par et affectation :

a=\dfrac{X+1}{X^3}=2

X=1

(X-1)^2

Multiplication par et affectation :

c=\dfrac{X+1}{(X-1)^2}=1

X=0

X^3

F_4-\dfrac{a}{(X-1)^2}-\dfrac{c}{X^3} = \dfrac{b}{X-1}+\dfrac{d}{X^2}+\dfrac{e}{X}

\Leftrightarrow F_4-\dfrac{2}{(X-1)^2}-\dfrac{1}{X^3} =\dfrac{-2X-3}{X^2(X-1)}= \dfrac{b}{X-1}+\dfrac{d}{X^2}+\dfrac{e}{X}

... on recommence

\dfrac{-2X-3}{X^2(X-1)}= \dfrac{b}{X-1}+\dfrac{d}{X^2}+\dfrac{e}{X}

Multiplication par et affectation :

d=\dfrac{-2X-3}{(X-1)}=3

X=0

X^2

Multiplication par et affectation :

X-1

X=1

b=\dfrac{-2X-3}{X^2}=-5

... dernière inconnue e ?

Affectation dans (*) d'une valeur qui ne soit pas un pôle

(*)

X=-1

\dfrac{1}{2}=-\dfrac{b}{2}+d-e

e=5

Méthode 1 Calcul des \( \lambda_k\)

Méthode 2 pour les pôles multiples

PREMIERS EXEMPLES

Méthode 1
Calcul des \( \lambda_k\)

Méthode 2
pour les pôles multiples

PREMIERS
EXEMPLES