Equation différentielle linéaire d'ordre 1
17/04/2024
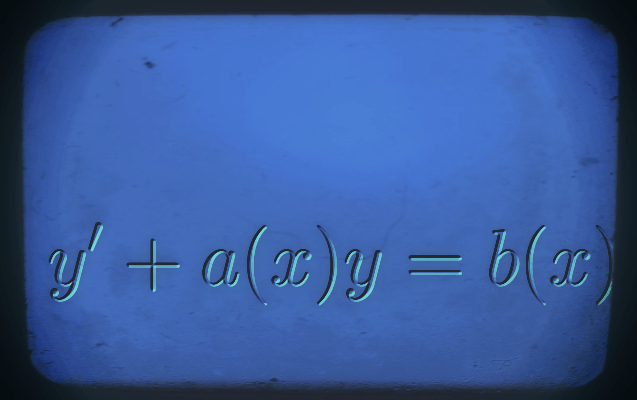
Equations différentielles linéaires d'ordre 1
Equation différentielle linéaire d'ordre 1
à coefficients constants
coefficient constant
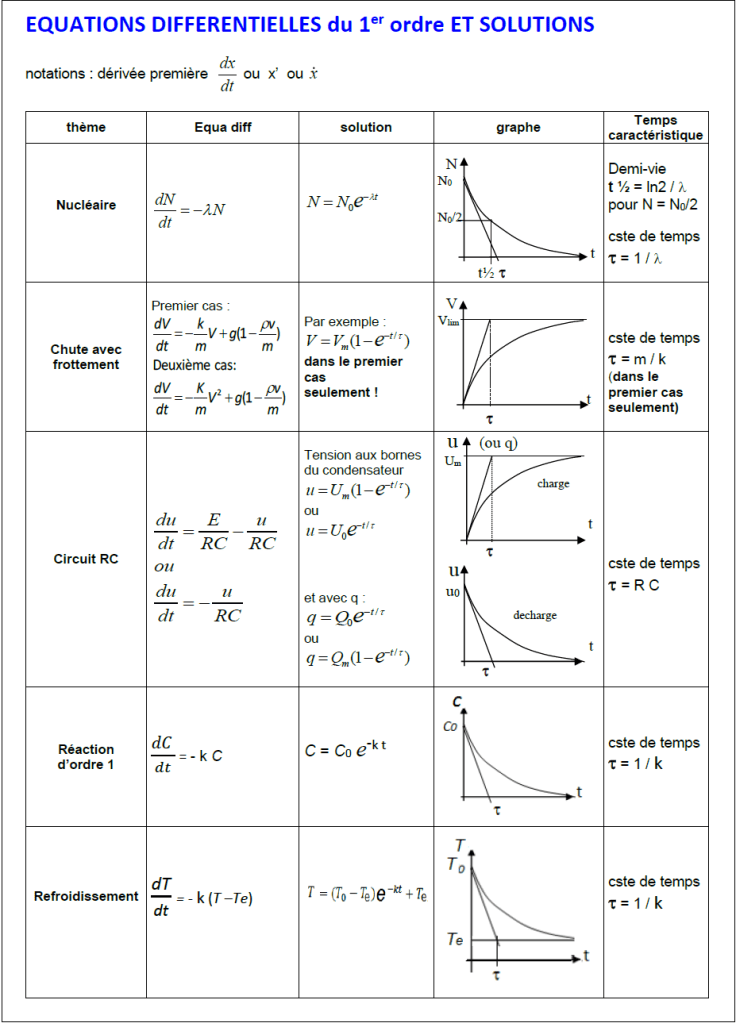
\( ay'+b y=0\)
Forme
\( y''+ay^2=b \)
\( ay'+b y=c \)
\( ay'+b y=0\)
\( ay'+b y=0\)
\( ay'+b y=0\)
Text
Coefficients a et b constants
\( ay'+b y=c \)
Equations différentielles linéaires d'ordre 1
Equations différentielles linéaires d'ordre 1
à coefficient constant
fonction de \( t \)

Cas de coefficients a et b non constants
loi de Newton du refroidissement
échauffement d’un objet dans un environnement variable
Equation différentielle linéaire d'ordre 1

Equation différentielle linéaire d'ordre 1

1. (\(E_1)\) : voir chapitre correspondant
3. \( (E_3) : \text{non sous la forme } y'+a(x)=b(x) \)
2. \( (E_2) : y'+a(x)y=b(x) \)
avec \( x\mapsto \dfrac{x^2+1}{x}\) et \( x\mapsto \dfrac{e^x}{x} \) continues sur l'ouvert \(]0;+\infty[\)
Equation différentielle linéaire d'ordre 1
Autrement dit
\( S_H \) est

un sous-espace vectoriel de
Equation différentielle linéaire d'ordre 1
Mieux.
\( S_H \) est

un sous-espace vectoriel de
Equation différentielle linéaire d'ordre 1

I est un intervalle ouvert
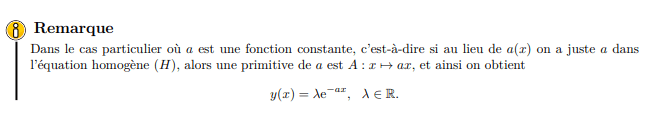
Equation différentielle linéaire d'ordre 1
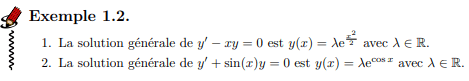
continue sur \( I=\mathbb{R}\)
continue sur \( I=\mathbb{R}\)
Equation différentielle linéaire d'ordre 1

Si \( a\) est constante et \( a\) est de la forme:
- \( x\mapsto P(x) \)
- \( x\mapsto P(x) e^{mx}\)
- \( x\mapsto A\cos(\omega x)+B\sin(\omega x) \)
}
Voir chapitre
où les
coefficients
sont constants
L'ensemble des solution de (E) est :
Equation différentielle linéaire d'ordre 1

Preuve : Existence de la fonction \( \lambda\) :
Soit \(x\mapsto b(x) e^{A(x)}\)
Cette fonction est définie sur I et est obtenue par produit et composition de fonctions continues donc elle est continue sur I
elle admet donc une primitive .
Soit \( \lambda \) une de ses primitives .
On considère \( y_p: x\mapsto \lambda (x) e^{-A(x)}\)
Equation différentielle linéaire d'ordre 1

Montrons que \(y_p\) est une solution de (E)
\( y_p: x\mapsto \lambda (x) e^{-A(x)}\)
Preuve (suite): Existence de la fonction \( \lambda\) :
Equation différentielle linéaire d'ordre 1
Soit \( \mathcal{S}\) l'ensemble des solutions de : \( (E) : y'+a(x)y=b(x) \)

Soit \( y_p\) une solution particulière de \( (E) \), on montre que:
Soit \( y \in \mathcal{S}\) :
On vérifie aisément que \( y-y_p \) est une solution particulière de \( (H) \)
En effet, \( y'+a(x)y=b(x) \)
et, \( y_p'+a(x)y_p=b(x) \)
(on soustrait membre à membre )
\( y-y_p \) est une solution de \( (H) \)
Réciproquement soit :
On a:
Sur I,il existe \( \lambda \in \mathbb{R}\) tel que \(y=\lambda e^{-A(x)}+y_p \)
Ainsi, \( y'+a(x)y=-a(x)\lambda e^{-A(x)}+y_p' +a(x) (\lambda e^{-A(x)}+y_p)\)
= \( -a(x)\lambda e^{-A(x)}-a(x)y_p+b(x) +a(x) (\lambda e^{-A(x)}+y_p)\)
\( y-y_p \) est une solution particulière de \( (H) \)
ainsi
On a montré que:
= \( b(x)\)
On a montré que:
Equation différentielle linéaire d'ordre 1
L'ensemble des solutions de (\(H\)) est :
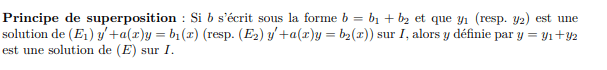
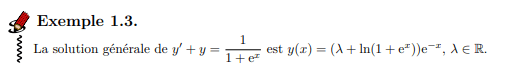
sont continues sur \(I=\mathbb{R}\)
Equation différentielle linéaire d'ordre 1
L' ensemble des solutions de (E) est :
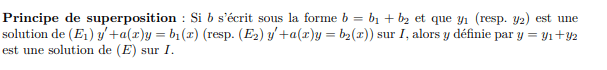
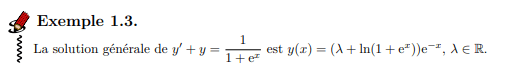
Solution particulière \(y_p\) :
donc

Equation différentielle linéaire d'ordre 1
\(a\) et \(b\) sont continues sur un intervalle ouvert I
Soit( \(x_0,y_0) \in I \times \mathbb{R}\)
Problème de
Cauchy-Lipschitz
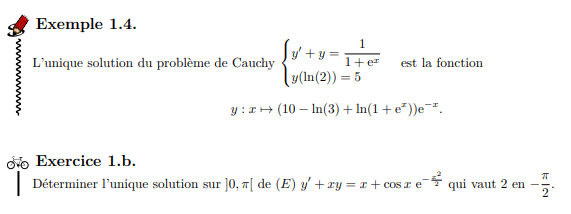
Résoudre l'équation différentielle suivante:
Equation différentielle linéaire d'ordre 1

Equation différentielle linéaire d'ordre 1
!!
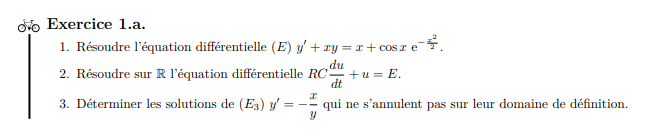
à faire
\((E_3)\\ \iff yy'=-x \\\iff \dfrac{1}{2}(y^2)'=-x \\ \iff (y^2)'=-2x\)
\(\iff y^2=-x^2+C\) avec C >0
\(\iff y=\sqrt{-x^2+C}\) sur \(I=]-\sqrt{C};\sqrt{C}[\)
\( y \) est dérivable sur I donc continue sur I, ainsi d' après la page précédente
à faire
\(\text{ ou } y=-\sqrt{-x^2+C}\) sur \(I=]-\sqrt{C};\sqrt{C}[\)