Equation différentielle linéaire d'ordre 1
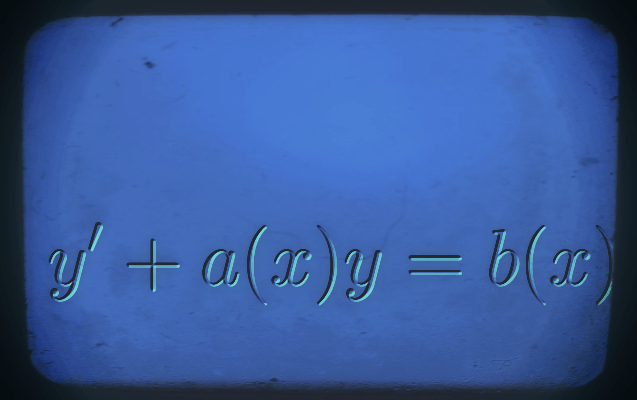
TD
\(a\) est continue
\(A\) est une primitive de \(a\)
\(b\) est continue
\(y_p\) est une solution particulière
Méthode de la variation de la constante:
On cherche \(y_p\) sous la forme \(y_p :x\mapsto \lambda(x) e^{-A(x)}\) avec \( \lambda\) dérivable sur \( I\)
\(a\) est continue
\(A\) est une primitive de \(a\)
\(b\) est continue
\(y_p\) est une solution particulière
Méthode de la variation de la constante:
On cherche \(y_p\) sous la forme \(y_p :x\mapsto \lambda(x) e^{-A(x)}\) avec \( \lambda\) dérivable sur \( I\)


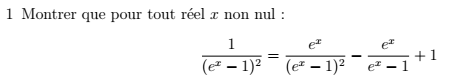
Exercice 4
Exercice 4
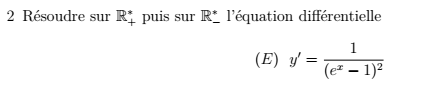
\(a\) est continue
\(A\) est une primitive de \(a\)
\(b\) est continue
\(y_p\) est une solution particulière
Méthode de la variation de la constante:
On cherche \(y_p\) sous la forme \(y_p :x\mapsto \lambda(x) e^{-A(x)}\) avec \( \lambda\) dérivable sur \( I\)
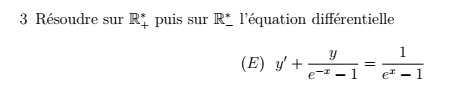
Exercice 4
\(a\) est continue
\(A\) est une primitive de \(a\)
\(b\) est continue
\(y_p\) est une solution particulière
Méthode de la variation de la constante:
On cherche \(y_p\) sous la forme \(y_p :x\mapsto \lambda(x) e^{-A(x)}\) avec \( \lambda\) dérivable sur \( I\)
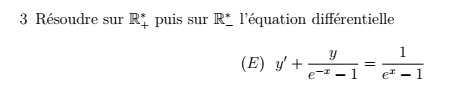
Exercice 4

\(a\) est continue sur \(\mathbb{R}\setminus\{1\}\)
donc \(I=]-\infty,1[\) ou \(I=]1,+\infty[\)

\(a\) est continue sur \(\ I\)
pour \(I=]1,+\infty[\)
pour \(I=]-\infty,1[\)

pour \(I=]1,+\infty[\)
pour \(I=]-\infty,1[\)
Méthode de la variation de la constante:
On cherche \(y_p\) sous la forme \(y_p :x\mapsto \lambda(x) e^{-A(x)}\) avec \( \lambda\) dérivable sur \( I\)

pour \(I=]1,+\infty[\)
pour \(I=]-\infty,1[\)

Soit
Existe -il un couple \( (\lambda,\mu) \) tel que \( \tilde{f}_{\lambda,\mu} \) soit de classe \(\mathcal{C_1}(\mathbb{R})\) ?

- \(f_{\lambda,\mu} \) est de classe \(\mathcal{C_1}(\mathbb{]-\infty;1[}) \)
- \(f_{\lambda,\mu} \) est de classe \(\mathcal{C_1}(\mathbb{]1;\infty[})\)
- \(\lim\limits_{x\to 1^-} \frac{e^{-x}}{x-1}=-\infty\)
- \(\lim\limits_{x\to 1^+} \frac{e^{-x}}{x-1}=+\infty\)
\( \tilde{f}_{0,0} \) est classe \(\mathcal{C_1}(\mathbb{R})\)
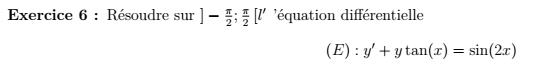
\(a\) est continue
\(A\) est une primitive de \(a\)
\(b\) est continue
\(y_p\) est une solution particulière
Méthode de la variation de la constante:
On cherche \(y_p\) sous la forme \(y_p :x\mapsto \lambda(x) e^{-A(x)}\) avec \( \lambda\) dérivable sur \( I\)
\(a\) est continue
\(A\) est une primitive de \(a\)
\(b\) est continue

Les intervalles I de travail sont \(]-\infty,0[\) et \(]0,+\infty[\)
Méthode de la variation de la constante:
On cherche \(y_p\) sous la forme \(y_p :x\mapsto \lambda(x) e^{-A(x)}\) avec \( \lambda\) dérivable sur \( I\)

Pour \(I=]-\infty,0[\)
Méthode de la variation de la constante:
On cherche \(y_p\) sous la forme \(y_p :x\mapsto \lambda(x) e^{-A(x)}\) avec \( \lambda\) dérivable sur \( I\)

Pour \(I=]0;+\infty[\)

Soit
On a trouvé :
Etape 1:Existe -il un couple \( (\lambda,\mu) \) tel que \( f_{\lambda,\mu} \) soit prolongeable par continuité en 0 .
Etape 2:Déterminer les couples tels que \( \tilde{f}_{\lambda,\mu} \) soit de classe \(\mathcal{C_1}(\mathbb{R})\) ?

Donc ,pour tout couple \((\lambda,\mu)\), il existe le prolongement par continuité suivant:

Existe -il un couple \( (\lambda,\mu) \) tel que \( \tilde{f}_{\lambda,\mu} \) soit de classe \(\mathcal{C_1}(\mathbb{R})\) ?
Etant issue d'opérations sur des fonctions de classe \(\mathcal{C_1}\)
\( \tilde{f}_{\lambda,\mu}\) est de classe \(\mathcal{C_1}\)
sur \(\mathbb{R}_-^*\) et sur sur \(\mathbb{R}_+^*\)
On sait que \( \tilde{f}_{\lambda,\mu} \) est de classe \(\mathcal{C_0}(\mathbb{R})\)
Etude de la dérivabilité en 0 avec des \(DL_1(0^-)\) et \(DL_1(0^+)\) et :
\( \tilde{f}_{\lambda,\mu} \) est dérivable en 0 si et seulement \( \lambda=\mu \)
\(a\) est continue
\(A\) est une primitive de \(a\)
\(b\) est continue


The end