Séquence 2

0
1
2
3
4
5
....
\(n\)
...

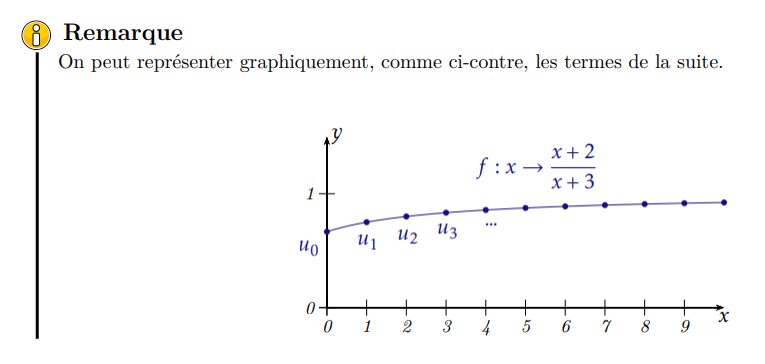
\(u_0\)
\(u_1\)
\(u_2\)
\(u_3\)
\(u_4\)
\(u_5\)
....
\(u_n\)
...

\(u\)

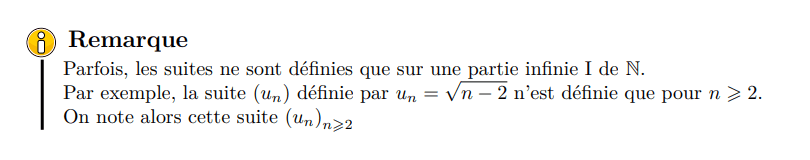
Autrement dit une suite peut être définie à partir de 1 ou 2 ou 3 ou....

-1

\(n^2-1\)

NE PAS CONFONDRE :
\(n\) ème terme et terme de rang \(n\)

Culture générale

Exemple malheureux:

\begin{equation*} \begin{array}{llll} f: & \R\setminus\lbrace-1\rbrace & \longrightarrow & \mathbb{R} \\ & x & \longmapsto & \dfrac{1}{x+1} \end{array} . \end{equation*}

\begin{equation*} \left\{\begin{array}{l} u_0 =-\dfrac{3}{2} \\ \forall n \in \mathbb{N} \quad u_{n+1}=\dfrac{1}{u_n+1} \end{array}\right. \end{equation*}

-\dfrac{3}{2}

-2

-1

\(u_0= \)
\(u_1=\)
\(u_2=\)
\(u_3=\)
\(u_4=\)

indéfini

\(f(I)\subset I\)

Exemple heureux:

\(f([-2;+\infty[)\) \(\subset\) \(\R_+\) \(\subset\) \([-2;+\infty[\)

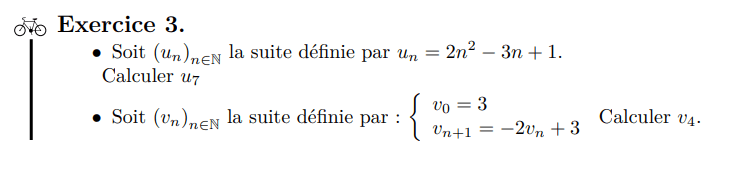
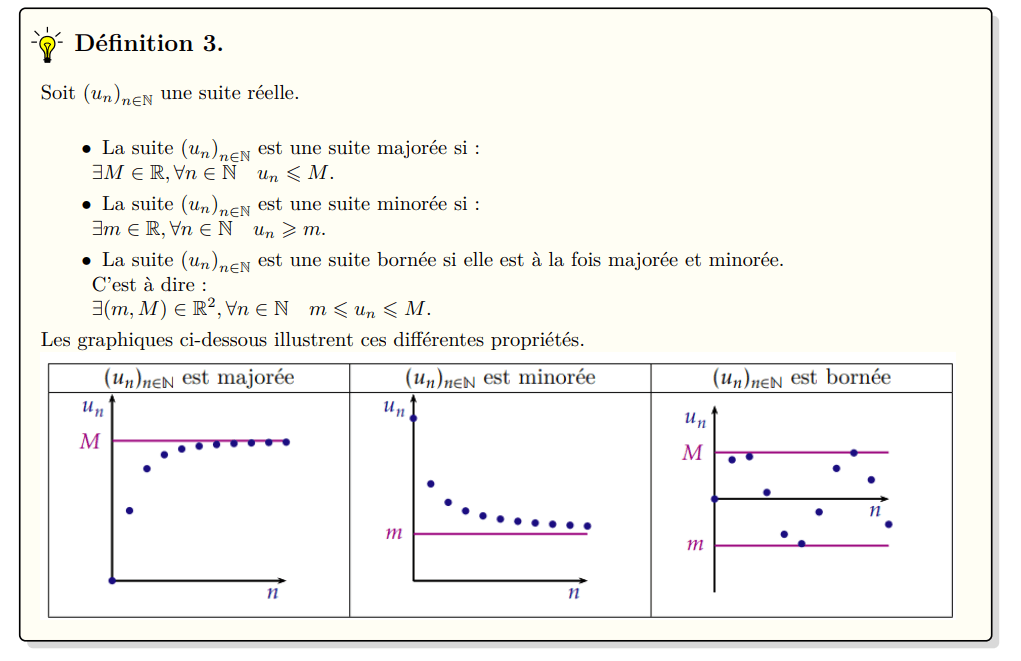
Suites majorées, minorées, bornées

Méthode plus automatique
(vue en classe):
On montre que
\(\forall n\in\N\), \( \dfrac{3n^2}{n^2+1}-3 \) est négatif.

preuve en classe

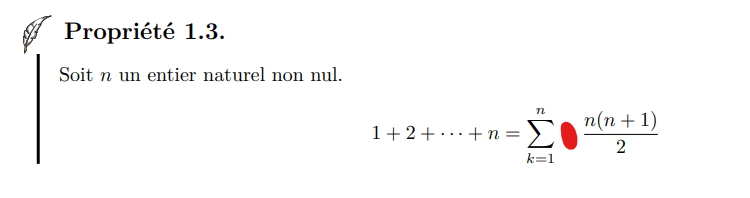
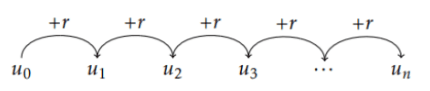
Car pour tout entier naturel \(n\),
\(u_{n+1}-u_n=r\)

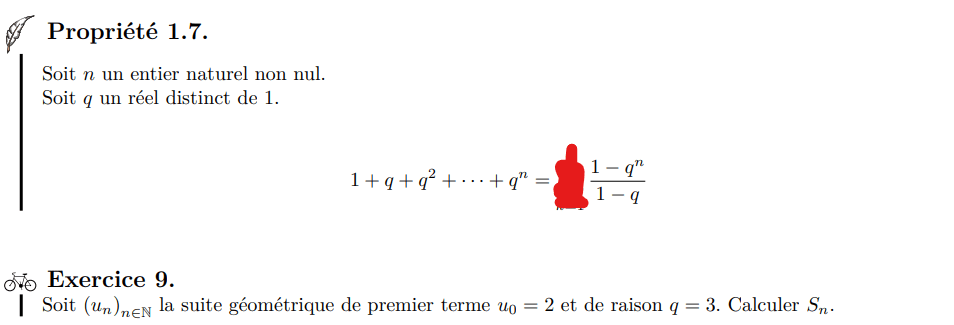
\(u_0= 2\)

\(u_1= 6\)

\(u_2= 18\)

\(u_3= 54\)

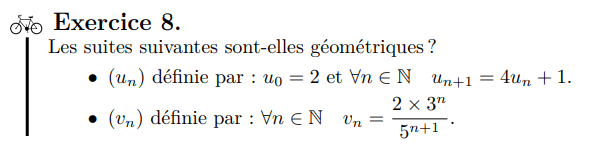
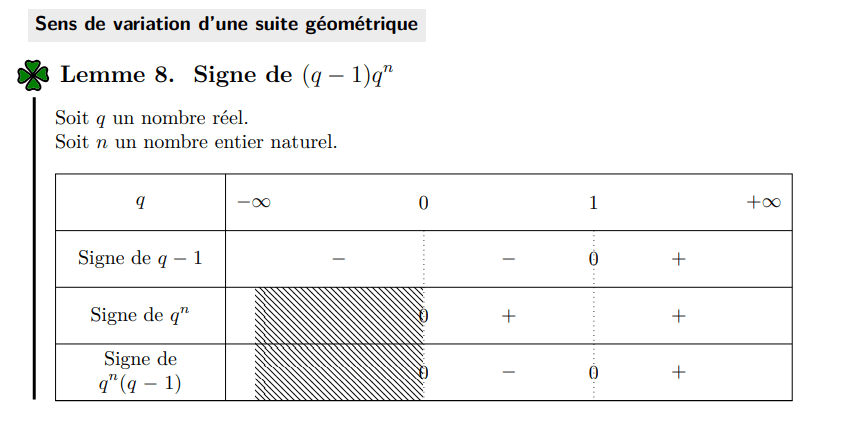
Méthode pratique:

Soit \(\left(u_n\right)_{n \in \mathbb{N}}\) la suite géométrique de premier terme \(u_0=-3\) et de raison \(q=\dfrac{4}{5}\).

Etudier les variations de cette suite.

On exprime \(u_n\) en fonction de \(n\):
\(\forall n\in \N, u_n=-3\left(\dfrac{4}{5}\right)^n\)

On étudie les variations de la suite\(\left(\left(\dfrac{4}{5}\right)^n\right)_{n\in\N}\)

Elle est décroissante car \(0<\frac{4}{5}<1\)

On conclut \(u_0\) est négatif que la suite \(\left(u_n\right)_{n \in \mathbb{N}}\) est CROISSANTE

Méthode pratique en 3 étapes

\(r^2=2r+\frac{5}{6}\)

Important