2/3 Maailmankaikkeuden suuret ja pienet rakenteet

FY01 Fysiikka luonnontieteenä

Maailmankaikkeuden ja aineen rakenteita

  • Maailmankaikkeuden eri asiat ja ilmiöt esiintyvät eri kokoluokissa
  • Tarvitaan järkeviä tapoja ilmaista todella suuria ja todella pieniä lukuja

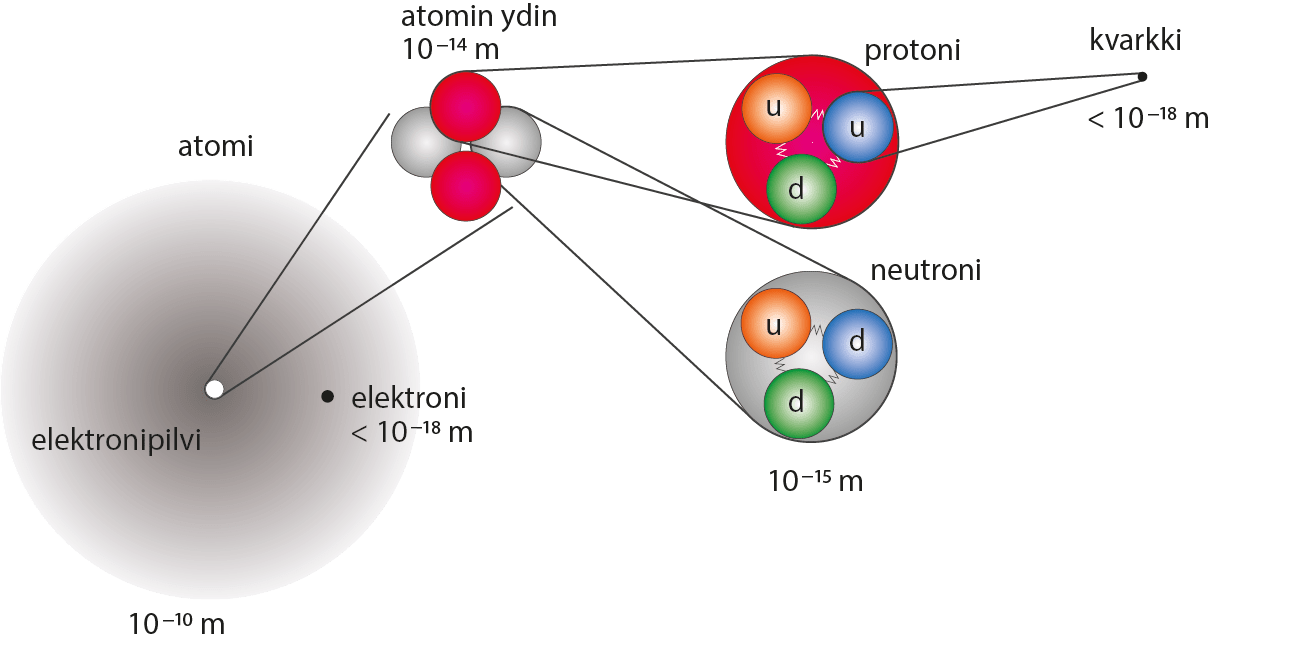
Kuva: Vipu 1-2 (Otava)

Kuva: Vipu 1-2 (Otava)

Linnunradan halkaisija: n. 9500000000000000 m

Protonin halkaisija: n. 0,0000000000000016 m

Linnunradan halkaisija: n. 9 500 000 000 000 000 m

Protonin halkaisija: n. 0,000 000 000 000 001 6 m

Universumin mittaskaalat

Jos Kuu olisi yksi pikseli

Kymmenen potenssit

  • Lukuarvojen ilmaiseminen perusyksiköissä (esim. metreinä tai sekunteina) tai auki kirjoitettuna ei ole aina järkevää
  • ​Suuria tai pieniä lukuja on helpompi esittää kymmenen potensseja tai kerrannaisyksiköitä (= etuliitteitä) käyttäen
    • ​Linnunradan halkaisija
    • Protonin halkaisija
9,5 \cdot 10^{15} \ \text m = 9,5 \cdot 10^{12} \ \text {km} = 9,5 \ \text {Pm}
1,6 \cdot 10^{-15} \ \text m = 1,6 \ \text {fm}

Elektronin massa:

m_e = 9{,}109 \ 3837 \cdot 10^{−31} \ \text{kg}
m_e = 0{,}000 \ 000 \ 000 \ 000 \ 000 \ 000 \ 000 \ 000 \ 000 \ 000 \ 910 \ 938 \ 37 \ \text{kg}
9{,}109 \ 3837 \cdot 10^{−31} \ \text{kg}

kerroin

kymmenen potenssi

eksponentti

yksikkö

10^4 = 1 \cdot 10 \cdot 10 \cdot 10 \cdot 10
10^{-4} = 1 \div 10 \div 10 \div 10 \div 10
= 1 \cdot \frac{1}{10} \cdot \frac{1}{10} \cdot \frac{1}{10} \cdot \frac{1}{10}

Kymmenpotenssin muuttaminen

  • Kun kymmenpotenssimuodosta halutaan tavallinen luku, siirretään pilkkua eksponentin verran
  • Jos eksponentti on positiivinen, siirretään pilkkua oikealle

 

 

  • Jos eksponentti on negatiivinen, siirretään pilkkua vasemmalle            
3,7 \cdot 10^4 \ \text {kg} \ ( = 3,7000 \cdot 10^4 \ \text {kg}) = 37 \ 000 \ \text {kg}
6,8 \cdot 10^{-5} \ \text {mm} \ ( = 000006,8 \cdot 10^{-5} \ \text {mm} ) = 0,000 \ 068 \ \text {mm}
  • Yksikkö luvun perässä pysyy samana

Kerrannaisyksiköt (etuliitteet)

  • Kerrannaisyksiköt ovat lyhyin tapa ilmaista hyvin suuria tai pieniä lukuja

 

 

 

  • Kaikille yksiköille (paitsi ajalle) käytetään samoja etuliitteitä: kilometri, kilojoule, kilonewton, kilogramma
  • Etuliitteet menevät kolmen kertaluvun hyppäyksin
    • Mega on tuhat kertaa suurempi kuin kilo
    • Nano on tuhat kertaa pienempi kuin mikro
  • Ilmoita lukuarvot mieluiten kerrannaisyksiköiden kymmenpotensseilla (kolmella jaollinen potenssi)!
1000 \ \text m = 10^3 \ \text m = 1 \cdot 10^3 \ \text m = 1 \ \text {km}
0,000 001 \ \text s = 10^{-6} \ \text s = 1 \cdot 10^{-6} \ \text s = 1 \ \mu \text s
73 \cdot 10^{-4} \ \text A
7,3 \cdot 10^{-3} \ \text A = 7,3 \ \text {mA}
(10^6 \ \text {vs.} \ 10^3)
(10^{-9} \ \text {vs.} \ 10^{-6})

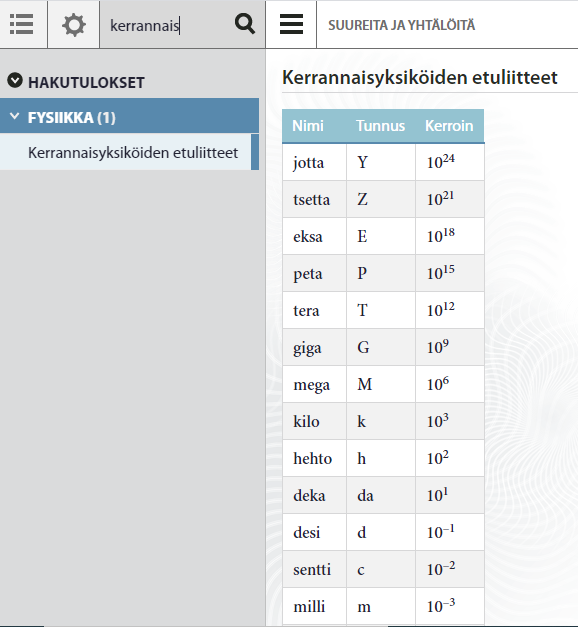
Kerrannaisyksiköt MAOL-taulukoissa

Positiiviset kymmenpotenssit usein isolla kirjaimella

 

Negatiiviset kymmenpotenssit pienillä kirjaimilla

mm vs. Mm

Mafy-taulukot

Pohdi kaverin kanssa

  1. Mene sivustolle Universumin mittaskaalat
  2. Kirjaa ylös vähintään yksi asia, esine tai ilmiö, jonka suuruusluokka on noin
    • 1 dekametri
    • 1 kilometri
    • 1 megametri
    • 1 gigametri
    • 1 petametri
    • 1 jottametri
  3. Mikä on suurin pituuden kokoluokka? Entä pienin? Ilmoita luvut kymmenpotenssimerkinnällä.
  4. Kuinka monta pölypunkkia mahtuisi peräkkäin, jos ne asetettaisiin jonoon jalkapallokentälle?
  • 1 senttimetri
  • 1 millimetri
  • 1 mikrometri
  • 1 nanometri
  • 1 attometri

Pohdi kaverin kanssa

Muunna tavalliset luvut kymmenpotensseiksi ja kerrannaisyksiköihin sekä kymmenpotenssit ja kerrannaisyksiköt tavallisiksi luvuiksi.

Ilmoita kaikki luvut siis kolmella eri tavalla!

4 \ 892 \ 000 \ 000 \ 000 \ 000 \ 000 \ 000 \ 000 \ 000 \ 000 \ \text g
350 \ \text {nm}
178 \cdot 10^{9} \ \text W
85 \cdot 10^{-12} \ \text J
0,000 \ 000 \ 42 \ \text s

2/3 Maailmankaikkeuden suuret ja pienet rakenteet

By pauliinak

2/3 Maailmankaikkeuden suuret ja pienet rakenteet

FY01 Fysiikka luonnontieteenä

  • 5

More from pauliinak