Décomposition en éléments simples de Fractions rationnelles
\mathbb{K}(X)
\mathbb{K} \text{=} \mathbb{R} \text{ ou } \mathbb{C}
14/04/2025
TD
F=\dfrac{\lambda_1}{X-3}+\dfrac{\lambda_2}{X+2}+\dfrac{\lambda_3}{X}
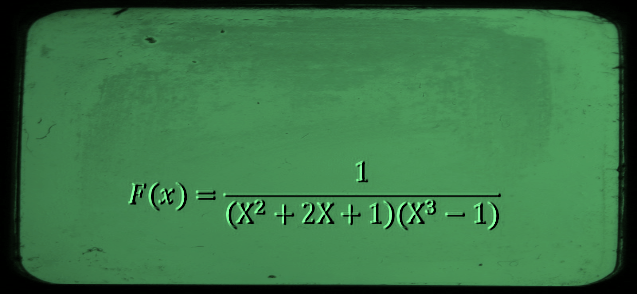
Tous les pôles sont simples
Multiplication par \(X-3\):
Multiplication par \(X+2\):
Multiplication par \(X\):
Avec l' affectation \(X=3\):
\lambda_1=\dfrac{X+1}{X(X+2)}
Avec l' affectation \(X=-2\):
Avec l' affectation \(X=0\):
\lambda_2=\dfrac{X+1}{X(X-3)}
\lambda_3=\dfrac{X+1}{(X-3)(X+2)}
\lambda_1=\dfrac{4}{15}
\lambda_2=-\dfrac{1}{10}
\lambda_3=-\dfrac{1}{6}
\( \alpha \) est un pôle donc
- D'après les formules de Taylor
D=D(\alpha)+D'(\alpha)(X-\alpha)+D^{(2)}(\alpha)\dfrac{(X-\alpha)^2}{2!}+\cdots+D^{(n)}(\alpha)\dfrac{(X-\alpha)^n}{n!} \text{ où } n=\deg(D)
D(\alpha)=0
D'(\alpha)\neq 0
Sinon \( \alpha \) est plus un pôle multiple
D=D'(\alpha)(X-\alpha)+D^{(2)}(\alpha)\dfrac{(X-\alpha)^2}{2!}+\cdots+D^{(n)}(\alpha)\dfrac{(X-\alpha)^n}{n!} \text{ où } n=\deg(D)
(X-\alpha)F=\dfrac{(X-\alpha)N}{D}=\lambda+(X-\alpha)G\\
\iff \dfrac{N}{\frac{D-D(\alpha)}{X-\alpha}}=\lambda+(X-\alpha)G\\
- Multiplication par \(X-\alpha\) membre à membre :
- On fait X tendre vers \(\alpha\) membre à membre :
\dfrac{N(\alpha)}{D'(\alpha)}=\lambda
\{ e^{\frac{2ik\pi}{n}} , k\in\llbracket 0,n-1\rrbracket \}
- Les pôles sont simples et correspondent aux racines n-ième de 1:
\lambda_k=\dfrac{e^{\frac{2ik\pi}{n}}+2}{ne^{\frac{2ik(n-1)\pi}{n}}}
\dfrac{X+2}{X^n-1}=\sum_{k=0}^{n-1} \dfrac{\lambda_k}{X-e^{\frac{2ik\pi}{n}}}
F=\dfrac{\lambda_1}{(X-1)^2}
+\dfrac{\lambda_2}{X-1}
+\dfrac{\lambda_3}{(X+1)^2}
+\dfrac{\lambda_4}{X+1}
La décomposition en éléments simples de F est :
Multiplication par \((X-1)^2\):
puis affectation \(X=1\):
\lambda_1=\dfrac{3}{4}
Calcul de \( \lambda_1\) et \( \lambda_2\) pour les éléments simples associés au pôle 1
F=\dfrac{3}{(X-1)^2(X+1)^2}
F-\dfrac{\lambda_1}{(X-1)^2}=\dfrac{\lambda_2}{(X-1)}+G
avec G défini en 1
\iff \dfrac{-3X^2-6X+9}{4(X-1)^2}=\dfrac{-3X-9}{4(X-1)(X+1)^2}=\dfrac{\lambda_2}{(X-1)}+G
Réduction de la multiplicité:
Multiplication par \((X-1)\) Avec l' affectation \(X=1\):
\lambda_2=-\dfrac{3}{4}
F=\dfrac{3}{4(X-1)^2}
-\dfrac{3}{4(X-1)}
+\dfrac{\lambda_3}{(X+1)^2}
+\dfrac{\lambda_4}{X+1}
La décomposition en éléments simples de F est :
Calcul de \( \lambda_3\) et \( \lambda_4\) pour les éléments simples associés au pôle -1
F=\dfrac{3}{(X-1)^2(X+1)^2}
MAiS NON
On pourrait faire comme pour \( \lambda_1\) et \( \lambda_2\)
Car on peut observer que \( F\) est paire \( F(X)=F(-X) \)
\lambda_1=\lambda_3=\dfrac{3}{4}
\lambda_4=-\lambda_2=\dfrac{3}{4}
F=\dfrac{3}{4(X-1)^2}
-\dfrac{3}{4(X-1)}
+\dfrac{3}{4(X+1)^2}
+\dfrac{3}{4(X+1)}
$$A= 1$$
$$B= (X-1)^3=X^3-3X^2+3X-1$$
B(0)=-1\neq 0
- On pose:
- Donc on peut effectuer une division suivant les puissances croissantes de A par B à l'ordre 3. Obtient le quotient
G_1\in\mathbb{R}(X) , G_1 \text{ définie en } 0
F=-\dfrac{1}{X^4}-\dfrac{3}{X^3}-\dfrac{6}{X^2}-\dfrac{10}{X}+G_1
$$Q_1=-1-3X-6X^2-10X^3$$
- On en déduit les éléments simples liés au pôle 0
$$A= 1$$
$$B= (Y+1)^3=Y^3+3Y^2+3Y+1$$
B(0)=1\neq 0
- Changement de variable Y=X-1
- Donc on peut effectuer une division suivant les puissances croissantes de A par à l'ordre 3. On obtient le quotient :
G_1\in\mathbb{R}(X) , G_1 \text{ définie en } 0
F=-\dfrac{1}{X^4}-\dfrac{3}{X^3}-\dfrac{6}{X^2}-\dfrac{10}{X}+G_1
F=-\dfrac{1}{(Y+1)Y^3}
$$Q_2=X^3+3X^2+3X+1$$
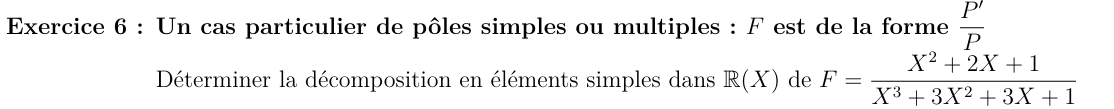
$$P=(X+1)^3$$
$$P'=3X^2+6X+3$$
$$P'=3(X^2+2X+1)=3(X+1)^2$$
$$P=X^3+3X^2+3X+1$$
F=\dfrac{1}{3} \dfrac{P'}{P}=\dfrac{1}{3} \dfrac{3}{X+1}=\dfrac{1}{X+1}
sans surprise !!
F= \dfrac{X^{n-1}}{X^n-2^n} , n>1
Autre exemple de DES à faire pour jeudi:
Méthode:
- On enchaîne des divisions euclidiennes de numérateurs\( N_i\) par P où \(P=X^2+X+1\)
F=\dfrac{N_1}{P^n}
\text{ avec }N_1=X^2+1
N_1=P N_2+R_1 \text{ avec } \deg(R_1)<\deg(P)
- Ainsi
F=\dfrac{N_2}{P^{n-1}}+\dfrac{R_1}{P^{n}}
\dfrac{R_1}{P^{n}} \text{ est un élément simple car } \deg R_1<\deg(P)
- On répète le procédé
N_2=P N_3+R_2 \text{ avec } \deg(R_2)<\deg(P)
- etc... Jusqu'à n'avoir que des éléments simples
\text{ Division euclidienne n°2}
- Ainsi
F=\dfrac{N_2}{P^{n-2}}+\dfrac{R_2}{P^{n-1}}+\dfrac{R_1}{P^{n}}
\text{ Division euclidienne n°1}
\dfrac{R_2}{P^{n-1}} \text{ est un 2ème élément simple car } \deg R_2<\deg(P)
F=\dfrac{\lambda_1}{X}+G \text{ avec } G\in \mathbb{R}(X) \text{ définie en 0}
\lambda_1=-1
- On multiple membre à membre par X puis on remplace X par 0
- On réduit la multiplicité du pôle 0
F-\dfrac{\lambda_1}{X}
\dfrac{N}{P^n}
sera de la forme
Et on poursuit la décomposition de comme dans l'exercice 7
F-\dfrac{\lambda_1}{X}
avec P irréductible et deg(P)=2
TD Fractions rationnelles
By intermaths.info
