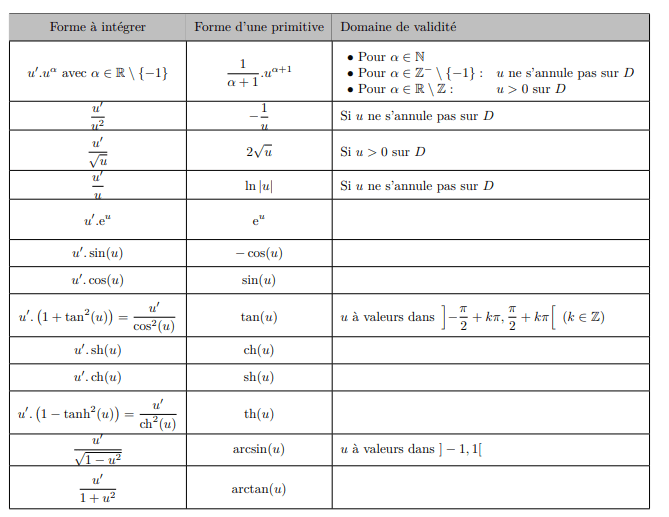
Intégration
Text
utiliser
Continuité uniforme
Rappel
La continuité est une propriéte locale pour une fonction
\(f\) est continue sur un intervalle \(I\)
\(\iff\)
\lim\limits_{x\to x_0} f(x)=f(x_0)
\(\iff\)
\forall \varepsilon >0, \exists \eta >0, \forall x \in I, \mid x-x_0\mid \leqslant \eta \Rightarrow \mid f(x)-f(x_0)\mid \leqslant \varepsilon
\forall x_0 \in I,
\forall x_0 \in I,
\forall \varepsilon >0, \exists \eta >0, \forall x \in I, \mid x-y\mid \leqslant \eta \Rightarrow \mid f(x)-f(y)\mid \leqslant \varepsilon
\forall y \in I,
\(\iff\)
\(\eta \) dépend de \(x\) et de \(\varepsilon\)
Continuité uniforme
Nouveau
La continuité uniforme est une propriéte globale pour une fonction
\(\iff\)
\(\eta \) ne dépend que de \(\varepsilon\)
\forall \varepsilon >0, \exists \eta >0, \forall (x,y) \in I^2, \mid x-y\mid \leqslant \eta \Rightarrow \mid f(x)-f(y)\mid \leqslant \varepsilon
Continuité uniforme
Exemple :
la fonction carré est continue sur \(\mathbb{R}\)
mais n'est pas uniformément continue sur \(\mathbb{R}\)
Remarque :
Il existe des fonctions continues sur un intervalle qui ne sont pas uniformement continue sur cet intervalle
Soit \(f:x \mapsto x^2\)
)
\forall \varepsilon >0, \exists \eta >0, \forall (x,y) \in\mathbb{R}^2, \mid x-y\mid \leqslant \eta \Rightarrow \mid f(x)-f(y)\mid \leqslant \varepsilon
Objectif :Montrons que :
\(f\) n'est pas uniformément continue sur \(\mathbb{R}\)
\( \iff \) non (
\exists \varepsilon >0, \forall \eta >0, \exists (x,y) \in\mathbb{R}^2, \mid x-y\mid \leqslant \eta \text{ et } \mid f(x)-f(y)\mid >\varepsilon
\( \iff \)
Soit \(\varepsilon=1\).
\(\forall \eta>0\) .
\text{ on a : } \mid x-y\mid=\frac{\eta}{2} \leqslant \eta \\ \text{ mais } \mid f(x)-f(y)\mid = \mid x^2-y^2\mid
=\frac{\eta}{2} \left(\frac{2}{\eta}+\frac{\eta}{2}\right)
=1+\frac{\eta^2}{4}> \varepsilon
\text{Soit } (x,y)=\left( \dfrac{1}{\eta}, \dfrac{1}{\eta}+\dfrac{\eta}{2} \right)
Continuité uniforme
1.Soit I un intervalle de \(\mathbb{R}\).
Soit \(x_0 \in I\).
Soit \(f\) une fonction uniformement continue sur \(I\)
Montrons que \(f\) est continue en \(x_0\)
Soit \(\varepsilon >0 \).
\(f\) étant uniformément continue sur \(I\).
\exists \eta >0, \forall (x,y) \in I^2, \mid x-y\mid \leqslant \eta \Rightarrow \mid f(x)-f(y)\mid \leqslant \varepsilon
\exists \eta >0, \forall x \in I, \mid x-x_0\mid \leqslant \eta \Rightarrow \mid f(x)-f(x_0)\mid \leqslant \varepsilon
En particulier,
Autrement dit, \(f\) est continue en \(x_0\)
Continuité uniforme
2.Soit I un intervalle de \(\mathbb{R}\).
Soit \(x_0 \in I\).
Soit \(f\) une fonction lipschitzienne sur \(I\)
Montrons que \(f\) est uniformément continue sur \( I\)
Soit \(\varepsilon >0 \).
\(f\) étant lipschitzienne sur \(I\)
\exists k \geqslant 0, \forall (x,y) \in I^2, \mid f(x)-f(y)\mid \leqslant k \mid x-y\mid
Autrement dit, \(f\) est uniformément continue sur \( I\)
\text{ Soit } \eta =\dfrac{\varepsilon}{k+1}>0 \text{; ainsi } k\eta =\dfrac{k\varepsilon}{k+1}<\varepsilon
\forall (x,y) \in I^2, \mid x-y\mid \leqslant \eta \Rightarrow \mid f(x)-f(y)\mid \leqslant k \mid x-y\mid \leqslant k \eta \leqslant \varepsilon
Continuité uniforme
Soit I =[a,b] un intervalle fermé borné de \(\mathbb{R}\).
Soit \(f\) une fonction continue sur [a,b]
Montrons que \(f\) est uniformément continue sur [a,b]
Raisonnement par l'absurde
Supposons \(f\) n'est pas uniformément continue sur [a,b]
\exists \varepsilon >0, \forall \eta >0, \exists (x,y) \in[a,b]^2, \mid x-y\mid \leqslant \eta \text{ et } \mid f(x)-f(y)\mid >\varepsilon
\exists \varepsilon >0, \forall n\in \mathbb{N^*}, \exists (x_n,y_n) \in [a,b]^2, \mid x_n-y_n \mid \leqslant \frac{1}{n} \text{ et } \mid f(x_n)-f(y_n)\mid >\varepsilon
En particulier :
Continuité uniforme
Avec le théorème de Bolzano -Weierstrass,
on pourra extraire simultanément(*)
deux suites convergentes dans [a,b]
\((x_{\phi(n)})_n\)et \((y_{\phi(n)})_n\)
\exists \varepsilon >0, \forall n\in \mathbb{N^*}, \exists (x_n,y_n) \in [a,b]^2, \mid x_n-y_n \mid \leqslant \frac{1}{n} \text{ et } \mid f(x_n)-f(y_n)\mid >\varepsilon
\text{Soit } \ell_x=\lim\limits_{n} x_{\phi(n)}
\text{Soit } \ell_y=\lim\limits_{n} y_{\phi(n)}
Continuité uniforme
\exists \varepsilon >0, \forall n\in \mathbb{N^*}, \exists (x_n,y_n) \in [a,b]^2, \mid x_n-y_n \mid \leqslant \frac{1}{n} \text{ et } \mid f(x_n)-f(y_n)\mid >\varepsilon
\ell_x=\lim\limits_{n} x_{\phi(n)}
\ell_y=\lim\limits_{n} y_{\phi(n)}
\forall n\in \mathbb{N^*}, \mid x_{\phi(n)}-y_{\phi(n)} \mid \leqslant \frac{1}{\phi(n)} \leqslant \frac{1}{n}
On fait \(n\) tendre vers \(+\infty \) :
0 \leqslant \mid \ell_x -\ell_y\mid \leqslant 0
\text{ donc } \ell_x=\ell_y
Continuité uniforme
\exists \varepsilon >0, \forall n\in \mathbb{N^*}, \exists (x_n,y_n) \in [a,b]^2, \mid x_n-y_n \mid \leqslant \frac{1}{n} \text{ et } \mid f(x_n)-f(y_n)\mid >\varepsilon
\ell_x=\lim\limits_{n} x_{\phi(n)}=\lim\limits_{n} y_{\phi(n)}= \ell_y
\(f\) étant continue sur \( I \):
0 \geqslant \varepsilon
f(\ell_x)=\lim\limits_{n} f(x_{\phi(n)})=\lim\limits_{n} f(y_{\phi(n)})= f(\ell_y)
\forall n\in \mathbb{N^*}, \mid f(x_{\phi(n)})-f(y_{\phi(n)}) \mid >\varepsilon
On fait \(n\) tendre vers \(+\infty \) :
\mid f(\ell_x)-f(\ell_y) \mid \geqslant \varepsilon
Contradiction !!!!
Continuité uniforme
Intégrale d'une fonction en escalier
Cas particulier
Intégrale d'une fonction en escalier
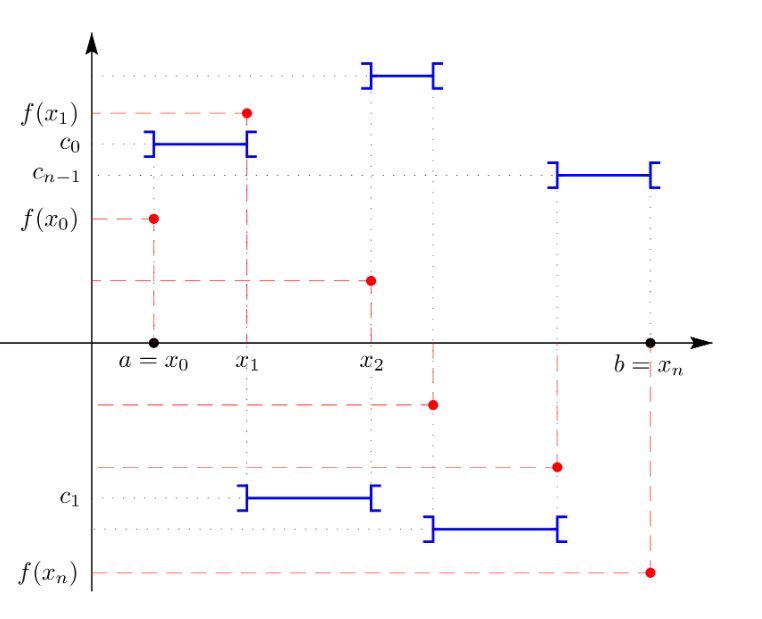
Intégrale d'une fonction en escalier
Notation avec les fonctions indicatrices
f(x)=\left\{\begin{aligned}
\sum_{i=0}^{n-1} c_i \mathbb{1}_{]x_i,x_{i+1}[} (x)& \textit{ si } x\in [a,b]\setminus\{x_i\}_{ 0 \leqslant i \leqslant n} \\
f(x_i) & \textit{ si } x\in \{x_i\}_{ 0 \leqslant i \leqslant n}
\end{aligned}\right.
Exemple connu de fonction en escalier
Intégrale d'une fonction en escalier
Intégrale d'une fonction en escalier
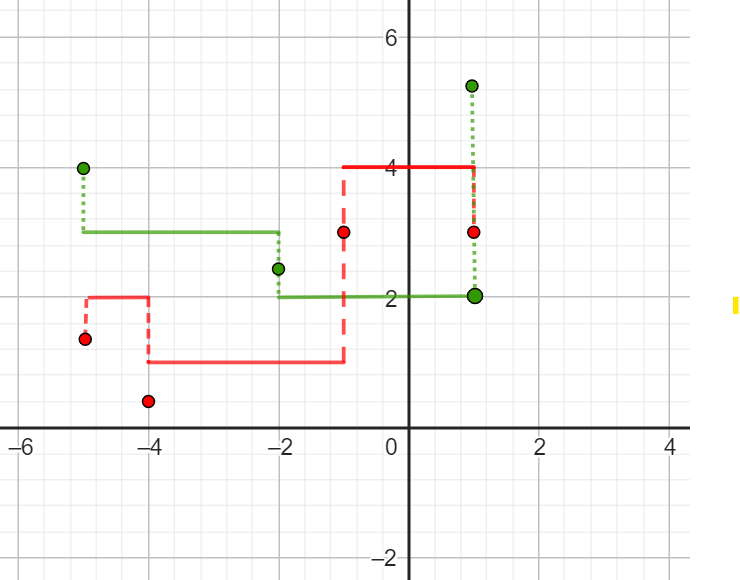
[a,b]=[-5,1]
\(\sigma_f=\{ -5;-4,-1;1\}\)
Intégrale d'une fonction en escalier
[a,b]=[-5,1]
\(\sigma_f=\{ -5;-4;-3;-1;0;1\}\)
Text
Ajout
Intégrale d'une fonction en escalier
[a,b]=[-5,1]
\(\sigma_f=\{ -5;-4,-1;1\}\)
\(\sigma_g=\{ -5;-2;1\}\)
\sigma_f\cup\sigma_g=\{ -5;-4;-2;-1;1\}
Intégrale d'une fonction en escalier
\text{Car constantes par morceaux au regard de la subdivision}\\
\sigma_f\cup\sigma_g
Intégrale d'une fonction en escalier
\text{Car constantes }\\
\text{par morceaux }\\
\text {au regard de la subdivision}\\
\sigma_f\cup\sigma_g
Intégrale d'une fonction en escalier
Soit \(\sigma_1=\{x_i\}_{0\leqslant i \leqslant n}\)
Indépendance de la subdivison
Soit \(\sigma_2=\{x'_i\}_{0\leqslant i \leqslant n}\)
Deux subdivisons adaptées de \(f\)
\text{On pose } I_{\sigma_1}=\sum_{i=0}^{n-1} y_i(x_{i+1}-x_i)
\text{ et } I_{\sigma_2}=\sum_{i=0}^{n-1} y_i(x'_{i+1}-x'_i)
\text{ montrons que : } I_{\sigma_1}=I_{\sigma_2}
Intégrale d'une fonction en escalier
Il existe \(i_0 \in \llbracket 0,n-1 \rrbracket \) tel que : \( x_{i_0} < y < x_{i_0+1}\)
Soit \( y \in [a,b]\) tel que \( y\notin \sigma_1\)
Soit \(\tilde{\sigma}=\sigma_1\cup \{y\}\)
\(x_0\)
\(x_n\)
\(x_{i_0+1}\)
\(x_{i_0}\)
\(y\)
\(x_{1}\)
Intégrale d'une fonction en escalier
- 1er bilan: \( I_{\sigma_1} \) reste inchangé si on lui ajoute un élément supplémentaire .
De proche en proche, on montre par ajout successif que \( I_{\sigma_1} =I_{\sigma_1 \cup \sigma_2} \)
\(x_0\)
\(x_n\)
\(x_{i_0+1}\)
\(x_{i_0}\)
\(y\)
\(x_{1}\)
\text{On pose } I_{\tilde{\sigma}}=\sum_{i=0}^{i_0-1} y_i(x_{i+1}-x_i)+y_{i_0}(y-x_{i_0})+y_{i_0}(x_{i_0+1}-y)+\sum_{i=i_0+1}^{n-1} y_i(x_{i+1}-x_i)
=\sum_{i=0}^{i_0-1} y_i(x_{i+1}-x_i)+y_{i_0}(x_{i_0+1}-x_{i_0})+\sum_{i=i_0+1}^{n-1} y_i(x_{i+1}-x_i)
=\sum_{i=0}^{n-1} y_i(x_{i+1}-x_i)
= I_{\sigma_1}
- 2ème bilan: De façon analogue , on montre que \( I_{\sigma_2} =I_{\sigma_2 \cup \sigma_1} \)
Conclusion :
on montre que \( I_{\sigma_1} =I_{\sigma_2} \)
Intégrale d'une fonction en escalier
1. On utilise \(\sigma =\sigma_f\cup \sigma_g =\{a_i\}_{0\leqslant i \leqslant n-1}\) une subdivision adaptée à \(f\) et \(g\)
2. On utilise l'inégalité triangulaire discrète :
\left \vert \sum_{i=0}^{n-1} z_i \right \vert \leqslant
\sum_{i=0}^{n-1} \mid z_i \mid
3. On utilise la relation :
\sum_{i=0}^{m} z_i + \sum_{i=m+1}^{n} z_i
=
\sum_{i=0}^{n} z_i
4. On utilise la relation 1.
Intégrale d'une fonction en escalier
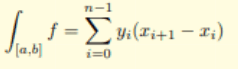
- Car c'est une somme de termes positifs
- On applique le 1. à la fonction positive \(x\mapsto g(x)-f(x)\) et on utilise la linéarité de l'intégrale
Fonction continue par morceaux
Fonction continue par morceaux
La fonction
x\mapsto \left\{\begin{aligned}
\dfrac{1}{x}&\textit{ si } x\neq 0 \\
0 & \textit{ si } x =0
\end{aligned}\right.
est-elle continue par morceaux ?
Fonction continue par morceaux
Existence de la norme infinie
\sup(A \cup B)=\max(\sup(A);\sup(B))
\bullet ~ \text{Propriété 1: Soient A et B deux sous-ensembles non vides et majorés de } \mathbb{R}.\\\text{leur réunion est majorée et }
\bullet ~ \text{Propriété 2(Généralisation): Soit} (A_i)_{i\in \llbracket 1;n \rrbracket } ~~\text{une famille de } n ~~\text{sous-ensemble non vides et majorées de }\mathbb{R}\\
\text{leur réunion est majorée et }
\sup(\bigcup_{i=1}^n A_i )=\max\limits_{i\in \llbracket 1;n \rrbracket }(A_i)
Si \(f\) est continue par morceaux, il existe une subdivision \( (x_i)_{i\in \llbracket 1;n\rrbracket} \) telle que \(f\) est prolongeable par continuité sur \([x_i;x_{i+1}]\) .\\
Pour justifier l'existence de la norme infinie en appliquant la propriété 2 et le théorème des bornes atteintes de Weierstrass avec :
A_i =f([x_i;x_{i+1}])
Fonction continue par morceaux
(détaillé en classe)
Fonction continue par morceaux
Remarque: Lorsque \(f\) est continue par morceaux , on applique le résultat démontré sur chaque segment \([x_i;x_{i+1}]\) puis on prolonge sur [a,b] chaque fonction \(\phi_p\)en escalier
\phi_p(x) =
\left\{\begin{array}{cl}
f(a) & \text { si } x=a \\
f(x_{i+1}) & \text { si } x \in ]x_i;x_{i+1}]
\end{array}\right.
Soit \( (x_i)_{i\in \llbracket 1;p\rrbracket} \) une subdivision de [a;b ]adaptée à \(f\).
On définit :
Eléments de la preuve
Prouvé en classe pour \(f\) continue sur [a,b]
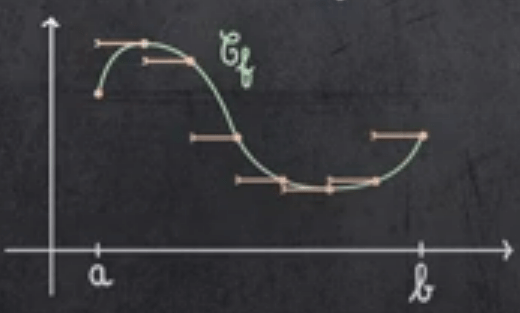
On a montré que : \( \lim\limits_{p} \Vert f-\phi_p\Vert _{\infty}=0\)
Grace au théorème de Heine sur
les segments \( [x_i;x_{i+1}] \).
Fonction continue par morceaux
\text {Interprétation: \\
L'ensemble des fonctions en escalier sur }[a, b] \text { à valeurs dans } \mathbb{K} \\
\text { est dense dans } \mathcal{C}_m([a, b], \mathbb{K}) \text {. }
Prouvé en classe pour \(f\) continue sur [a,b]
Intégrale d’une fonction continue par morceaux
Problématique
Fonction continue par morceaux
\text {Les 2 suites } \left(\int_{[a, b]} \mathcal{s}_n \right)_n \text {~~et~~ }\left(\int_{[a, b]} \mathcal{S}_n \right)_n \text{ sont ADJACENTES}
On choisit une subdivision régulière de [a;b] \( (x_i)_{i\in \llbracket 1;n\rrbracket} \) ainsi :\( x_{i+1}-x_i=\dfrac{b-a}{n}\)
\int_{[a, b]} (\phi_p ) =\sum_{i=0}^{p-1}(x_{i+1}-x_i) y_{p,i}=\frac{b-a}{p}\sum_{i=0}^{p-1} f\left(\frac{x_{i}+x_{i+1}}{2}\right)
Etape1 : On considère Les suites de fonctions en escaliers \((\mathcal{s}_n)_n\in\N^*\) et \((\mathcal{S}_n)_n\in\N^*\) définies par:
\mathcal{s}_n(x) =
\left\{\begin{array}{cl}
f(a) & \text { si } x=a \\
m_i & \text { si } x \in ]x_i;x_{i+1}]
\end{array}\right.
\mathcal{S}_n(x) =
\left\{\begin{array}{cl}
f(a) & \text { si } x=a \\
M_i & \text { si } x \in ]x_i;x_{i+1}]
\end{array}\right.
Où \(M_i\) (resp. \(m_i\))est la borne supérieure (resp. inférieure) de \(f\) sur \([x_i;x_{i+1}]\)
Ces deux suites de On considère Les suites de fonctions en escaliers \((\mathcal{s}_n)_n\in\N^*\) et \((\mathcal{S}_n)_n\in\N^*\) définies par:
On les nomme "sommes de Darboux "
\text {Les 2 suites } \left(\int_{[a, b]} \mathcal{s}_n \right)_n \text {~~et~~ }\left(\int_{[a, b]} \mathcal{S}_n \right)_n \text{ convergent donc}\\
\text{ vers une même limite réelle~} \ell_f
\int_{[a, b]} (\phi_p ) =\sum_{i=0}^{p-1}(x_{i+1}-x_i) y_{p,i}=\frac{b-a}{p}\sum_{i=0}^{p-1} f\left(\frac{x_{i}+x_{i+1}}{2}\right)
Etape 2 : On démontre la convergence vers \(\ell_f\) de
\int_{[a, b]} \phi_n =\frac{b-a}{n}\sum_{i=0}^{n-1} \phi_n\left(\frac{x_{i}+x_{i+1}}{2}\right)
\left( \int_{[a, b]} \phi_n \right)_n
\int_{[a, b]} \mathcal{S}_n =\frac{b-a}{n}\sum_{i=0}^{n-1} M_i
\left \vert \int_{[a, b]} \phi_n -\int_{[a, b]} \mathcal{S}_n \right \vert
= \left \vert \frac{b-a}{n}\sum_{i=0}^{n-1} \phi_n\left(\frac{x_{i}+x_{i+1}}{2}\right) -M_i\right \vert
\int_{[a, b]} (\phi_p ) =\sum_{i=0}^{p-1}(x_{i+1}-x_i) y_{p,i}=\frac{b-a}{p}\sum_{i=0}^{p-1} f\left(\frac{x_{i}+x_{i+1}}{2}\right)
\left \vert \int_{[a, b]} \phi_n -\int_{[a, b]} \mathcal{S}_n \right \vert
\leqslant \frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert \phi_n\left(\frac{x_{i}+x_{i+1}}{2}\right) -
M_i\right \vert
\leqslant \frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert (\phi_n-f)\left(\frac{x_{i}+x_{i+1}}{2}\right) \right \vert
+
\frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert f\left(\frac{x_{i}+x_{i+1}}{2}\right) -
f\left(c_i\right) \right \vert
= \left \vert \frac{b-a}{n}\sum_{i=0}^{n-1} \phi_n\left(\frac{x_{i}+x_{i+1}}{2}\right) -
\frac{b-a}{n}\sum_{i=0}^{n-1} M_i\right \vert
Pour tout entier naturel \(n\) non nul,
inégalité triangulaire
\leqslant \frac{b-a}{n}\sum_{i=0}^{n-1} \left \Vert \phi_n\ -
f\right \Vert_{\infty}
+
\frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert f\left(\frac{x_{i}+x_{i+1}}{2}\right) -
f\left(c_i\right) \right \vert
\leqslant \frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert \phi_n\left(\frac{x_{i}+x_{i+1}}{2}\right) -
f\left(\frac{x_{i}+x_{i+1}}{2}\right)\right \vert
+
\frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert f\left(\frac{x_{i}+x_{i+1}}{2}\right) -
M_i \right \vert
Théorème des Bornes atteintes
\int_{[a, b]} (\phi_p ) =\sum_{i=0}^{p-1}(x_{i+1}-x_i) y_{p,i}=\frac{b-a}{p}\sum_{i=0}^{p-1} f\left(\frac{x_{i}+x_{i+1}}{2}\right)
\left \vert \int_{[a, b]} \phi_n -\int_{[a, b]} \mathcal{S}_n \right \vert
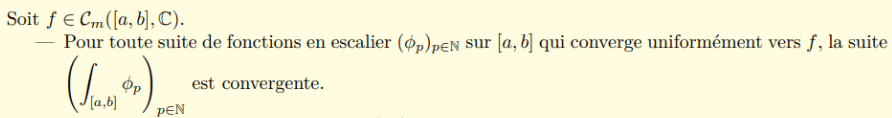
Pour tout entier naturel \(n\) non nul,
\leqslant \frac{b-a}{n}\sum_{i=0}^{n-1} \left \Vert \phi_n\ -
f\right \Vert_{\infty}
+
\frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert f\left(\frac{x_{i}+x_{i+1}}{2}\right) -
f\left(c_i\right) \right \vert
\leqslant (b-a)\left \Vert \phi_n\ -
f\right \Vert_{\infty}
+
\frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert f\left(\frac{x_{i}+x_{i+1}}{2}\right) -
f\left(c_i\right) \right \vert
(1)
De plus, pour tout
i \in \llbracket 1,n-1\rrbracket
\left \vert \frac{x_{i}+x_{i+1}}{2} -
c_i \right \vert \leqslant \frac{b-a}{n}
(2)
\int_{[a, b]} (\phi_p ) =\sum_{i=0}^{p-1}(x_{i+1}-x_i) y_{p,i}=\frac{b-a}{p}\sum_{i=0}^{p-1} f\left(\frac{x_{i}+x_{i+1}}{2}\right)
\left \vert \int_{[a, b]} \phi_n -\int_{[a, b]} \mathcal{S}_n \right \vert
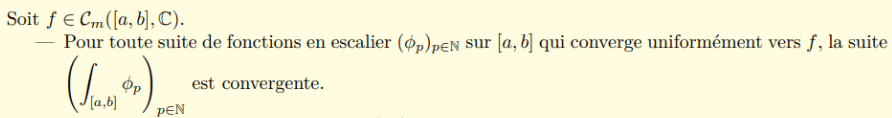
Pour tout entier naturel \(n\) non nul,
\leqslant (b-a)\left \Vert \phi_n\ -
f\right \Vert_{\infty}
+
\frac{b-a}{n}\sum_{i=0}^{n-1} \left \vert f\left(\frac{x_{i}+x_{i+1}}{2}\right) -
f\left(c_i\right) \right \vert
Soit \(\varepsilon >0\).
f est continue par prolongement sur chaque \( [x_i;x_{i+1}] \).
donc f est uniformement continue sur chaque \( [x_i;x_{i+1}] \).
Théorème de
Heine
\exists \eta_i >0, \forall (x,y) \in [x_i;x_{i+1}]^2, \mid x-y\mid \leqslant \eta_i\Rightarrow \mid f(x)-f(y)\mid \leqslant \dfrac{\varepsilon}{2(b-a)}
\text{On considère }\eta=\min\limits_{i\in \llbracket 1;n-1 \rrbracket }(\eta_i)
\exists N_0 \in \mathbb{N} , \forall n \geqslant N_0 ,\Vert \phi_n-f \Vert_{\infty} \leqslant \dfrac{\varepsilon}{2(b-a)}
Hypothèse de convergence uniforme vers f
continuité uniforme
(3)
(4)
(1)
\left \vert \frac{x_{i}+x_{i+1}}{2} -
c_i \right \vert \leqslant \frac{b-a}{n}
(2)
\int_{[a, b]} (\phi_p ) =\sum_{i=0}^{p-1}(x_{i+1}-x_i) y_{p,i}=\frac{b-a}{p}\sum_{i=0}^{p-1} f\left(\frac{x_{i}+x_{i+1}}{2}\right)
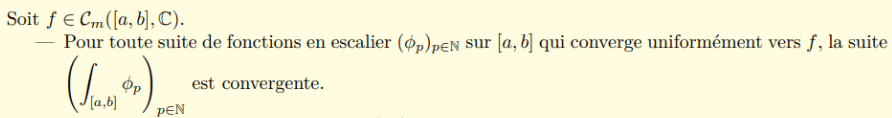
On choisit \(N_1=\max(N_0,\dfrac{b-a}{\eta})\).
d'après (1),(2), (3) et (4) on a:
Ainsi, pour tout entier naturel \(n \geqslant N_1\) on a :
\(n \geqslant N_0\) et \(n \geqslant \dfrac{b-a}{\eta} \iff \dfrac{b-a}{n}\leqslant \eta \)
Pour tout entier naturel \(n \geqslant N_1\)
Conclusion:
\text{Pour tout } n \in \N , \left \vert \int_{[a, b]} \phi_n - \ell_f \right \vert \leqslant \left \vert \int_{[a, b]} \phi_n - \int_{[a, b]} \mathcal{S}_f \right \vert
+\left \vert \int_{[a, b]} \mathcal{S}_f - \ell_f \right \vert
\left \vert \int_{[a, b]} \phi_n -\int_{[a, b]} \mathcal{S}_n \right \vert \leqslant \dfrac{\varepsilon}{2}+\dfrac{\varepsilon}{2}
\lim\limits_n \left \vert \int_{[a, b]} \phi_n -\int_{[a, b]} \mathcal{S}_n \right \vert =0
\text{Donc~~~}\lim\limits_n \left \vert \int_{[a, b]} \phi_n -\ell_f\right \vert =0
\( \lim\limits_{p} \Vert f-\phi_p\Vert_{\infty}=0\)
On a vue que la limite \(\ell_f\) dépend des sommes de Darboux qui ne dépendent QUE de \(f\)
Fonction continue par morceaux
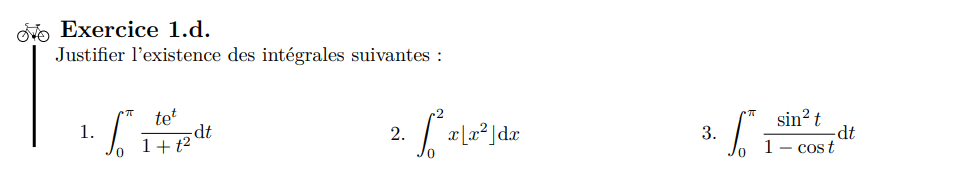
Fonction continue par morceaux
(x+iy)\int_a^b \mathrm{e}^{(x+\mathrm{i} y) t} \mathrm{~d} t=\left[\frac{1}{x+\mathrm{i} y} \mathrm{e}^{(x+\mathrm{i} y) t}\right]_a^b
=(x+iy)\int_a^b \left(~~ \mathrm{e}^{xt} \cos(yt) + i \mathrm{e}^{xt} \sin(yt) ~~\right)\mathrm{~d} t
=(x+iy)\int_a^b \mathrm{e}^{xt} \cos(yt) \mathrm{~d} t + i (x+iy) \int_a^b \mathrm{e}^{xt} \sin(yt) \mathrm{~d} t
=(x+iy)\int_a^b \mathrm{e}^{xt} \cos(yt) \mathrm{~d} t + i (x+iy) \int_a^b \mathrm{e}^{xt} \sin(yt) \mathrm{~d} t
=x\int_a^b \mathrm{e}^{xt} \cos(yt) \mathrm{~d} t +
iy\int_a^b \mathrm{e}^{xt} \cos(yt) \mathrm{~d} t +
i x \int_a^b \mathrm{e}^{xt} \sin(yt) \mathrm{~d} t
-y \int_a^b \mathrm{e}^{xt} \sin(yt) \mathrm{~d} t
=\int_a^b \dfrac{d}{dt}(\mathrm{e}^{xt}) \cos(yt) \mathrm{~d} t
+
i\int_a^b \mathrm{e}^{xt} \dfrac{d}{dt}(\sin(yt)) \mathrm{~d} t +
i \int_a^b \dfrac{d}{dt}(\mathrm{e}^{xt}) \sin(yt) \mathrm{~d} t
+ \int_a^b \mathrm{e}^{xt} \dfrac{d}{dt}(\cos(yt)) \mathrm{~d} t
=\left[\mathrm{e}^{(x+\mathrm{i} y) t}\right]_a^b
=
\left[ \mathrm{e}^{xt} \cos(yt)\right]_a^b
-
\int_a^b \mathrm{e}^{xt} \dfrac{d}{dt}(\cos(yt)) \mathrm{~d} t
+
i
\left[ \mathrm{e}^{xt} \sin(yt)\right]_a^b
-i\int_a^b \dfrac{d}{dt}(\mathrm{e}^{xt}) \sin(yt) \mathrm{~d} t \\+
i \int_a^b \dfrac{d}{dt}(\mathrm{e}^{xt}) \sin(yt) \mathrm{~d} t
+ \int_a^b \mathrm{e}^{xt} \dfrac{d}{dt}(\cos(yt)) \mathrm{~d} t
=
\left[ \mathrm{e}^{xt} \cos(yt)\right]_a^b
+
i
\left[ \mathrm{e}^{xt} \sin(yt)\right]_a^b
=
\left[ \mathrm{e}^{xt} \cos(yt)
+
i
\mathrm{e}^{xt} \sin(yt)\right]_a^b
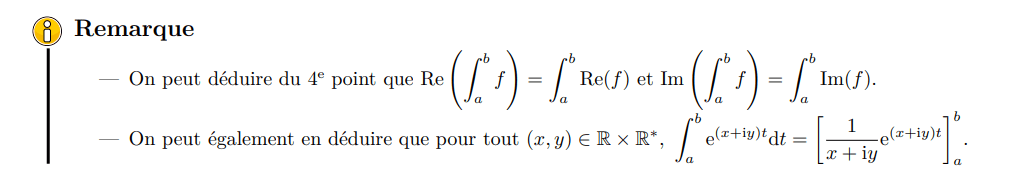
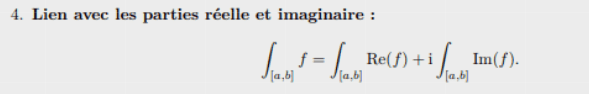
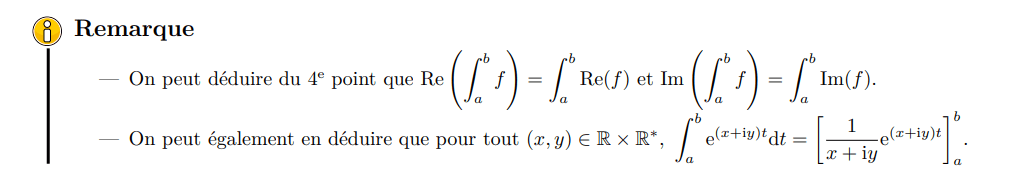
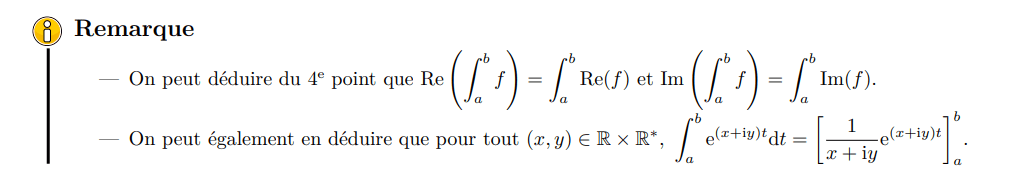
voir TD
Fonction continue par morceaux
voir TD
Fonction continue par morceaux
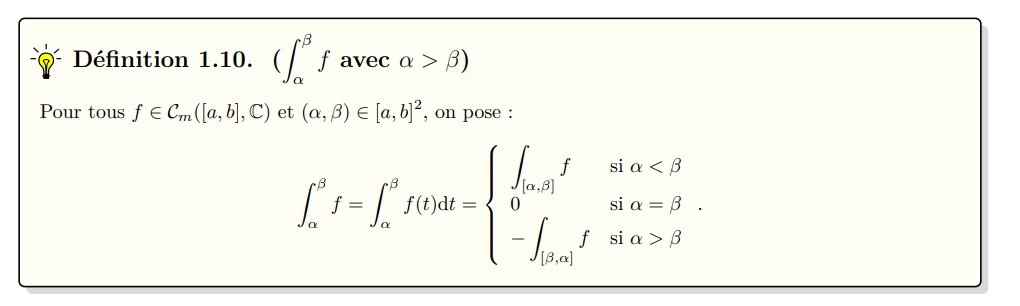
Théorèmes de la moyenne
Théorèmes de la moyenne
généralisé en TD
Limite d'intégrales
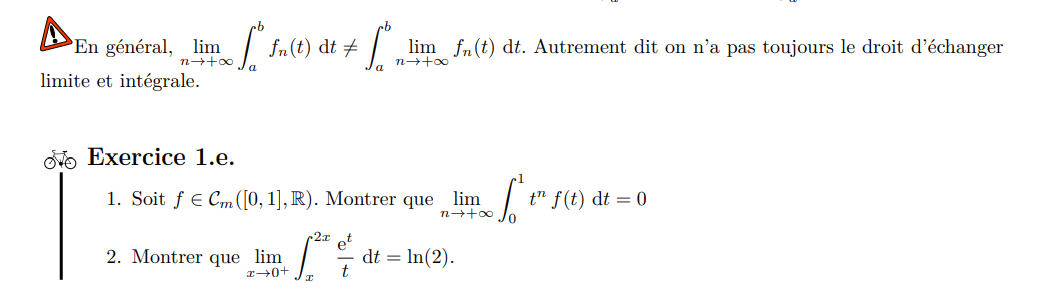
Intégration et dérivation
Intégration et dérivation
Intégration et dérivation
Intégration et dérivation
Théoreme fondamental de l'analyse
Le théorème fondamental de l'analyse montre que :
les fonctions définies par des intégrales de la forme \(x \mapsto \int_a^x f(t) \mathrm{d} t\)
sont dérivables (et même de dérivée continue).
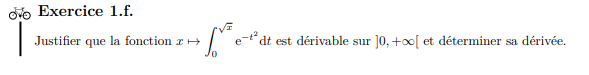
Théoreme fondamental de l'analyse
Théoreme fondamental de l'analyse
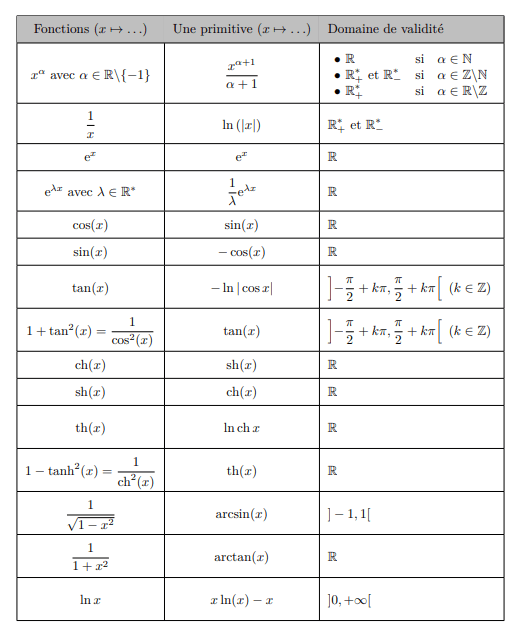
Intégration par parties
Changement de variables
Changement de variables
De plus si \(\varphi\) est une bijection de I sur J.
\forall (c,d)\in J^2, \int_{c}^{d} f(x) \mathrm{d} x =\int_{\varphi^{-1}(c)}^{\varphi^{-1}(d)} f(\varphi(t)) \varphi^{\prime}(t) \mathrm{d} t
Changement de variables
\text { Déterminer } \int_{\frac{\pi^2}{4}}^{\pi^2} \cos (\sqrt{x}) \mathrm{d} x
\text {Déterminer les primitives de } x \mapsto \cos (\sqrt{x}) \text { sur } ] 0,+\infty[
Exemple:
Parité et périodicité
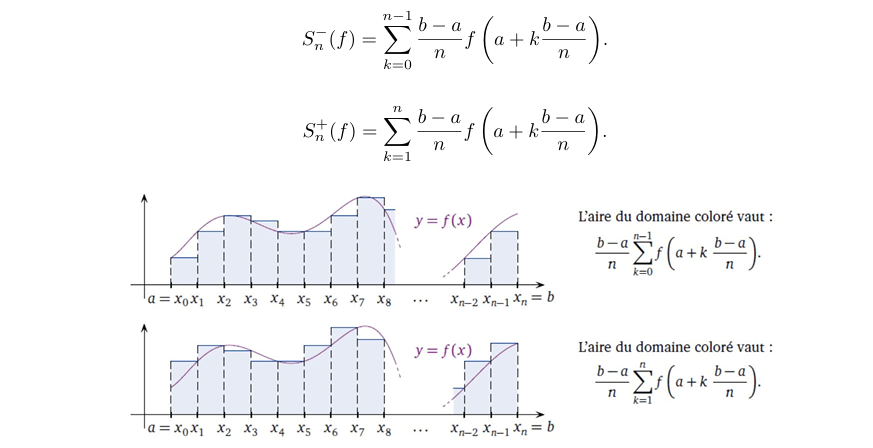
Approximation par les sommes de Rieman
INTEGRATION_DEMONSTRATIONS
By intermaths.info
