Séquence 1

Dans cette séquence, sont rappelées les notions et techniques vues au lycée, pour calculer, manipuler des expressions littérales, résoudre des équations ou inéquations... Dans le dernier paragraphe, nous abordons quelques notions de logique avec l’utilisation des quantificateurs et des connecteurs logique

Séquence 1

\(\sqrt{49}\)

2

\(10^3\)

\(\dfrac{21}{7}\)

\(\dfrac{-25}{-5}\)

\N

-7

\(-\sqrt{121}\)

\mathbb{Z}

-3,14

\(10^{-5}\)

\(\dfrac{1}{4}\)

\mathbb{D}

\(\dfrac{1}{3}\)

\(-\dfrac{\sqrt{4}}{7}\)

\mathbb{Q}

\(\sqrt{2}\)

\(\pi\)

\(e\)

\mathbb{R}

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.1 Ensembles de nombres

1.1.1 Les ensembles usuels de nombres

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.1 Ensembles de nombres

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.1 Ensembles de nombres

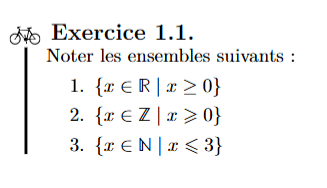
Réponses:

1.\quad \{x\in\R\mid x\geqslant 0\} =
2.\quad \{x\in\Z\mid x\geqslant 0\} =
3.\quad \{x\in\N\mid x\leqslant 3\} =
\R_+
\N
\{0,1,2,3\}

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.1 Ensembles de nombres

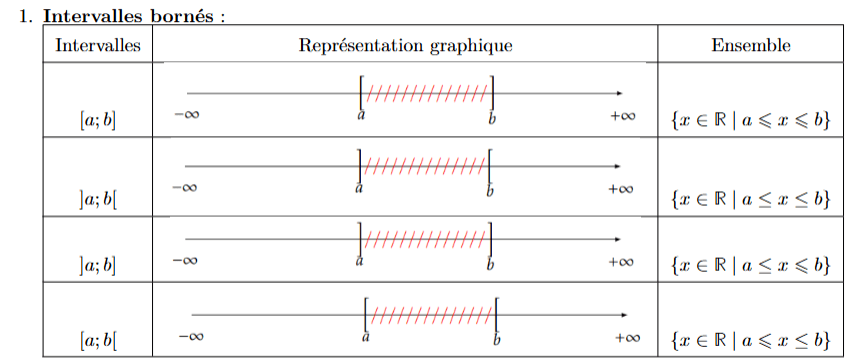
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.1 Ensembles de nombres

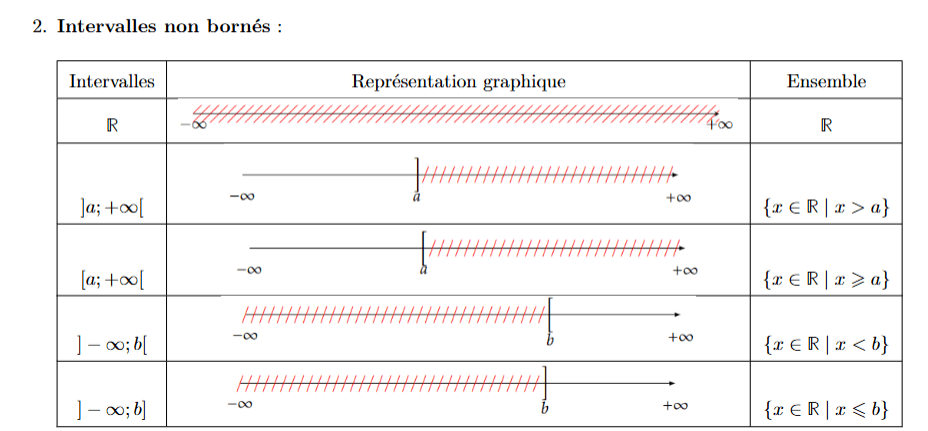
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.1 Ensembles de nombres

\(\varnothing\)

Ensemble vide :

\{2n \mid n \in \Z\}\cap \{ 2n+1\mid n \in \Z \}=
\{x\in \R \mid x^2+2=0\}=

\(\varnothing\)

\(\varnothing\)

\(\varnothing\)

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.1 Ensembles de nombres

\llbracket -3;4 \rrbracket =
\{ -3;-2;-1;0;1;2;3;4\}

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.1 Ensembles de nombres

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

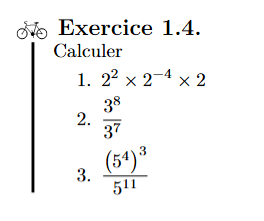
1.2 Quelques règles indispensables

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

  • Ecriture sans radical 
  • Ecriture sous la forme \(a\sqrt{b}\)
  • Calcul 
\left(\sqrt{3-\sqrt{7}}\right)^2=
3-\sqrt{7}
\sqrt{72}=
6\sqrt{2}
\sqrt{\frac{63}{7}}=
3
\frac{2}{\sqrt{3}}=
\frac{2\sqrt{3}}{3}

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

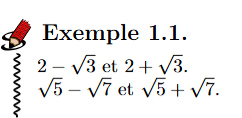
sont des expressions conjuguées

Les racines d'un trinôme \(ax^2+bx+c\) 

1.2 Quelques règles indispensables

\dfrac{-b-\sqrt{\Delta}}{2a}
\dfrac{-b+\sqrt{\Delta}}{2a}

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

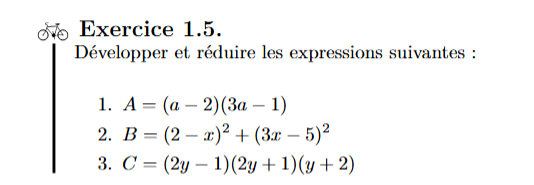
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

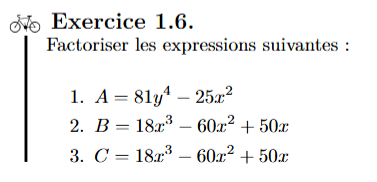
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

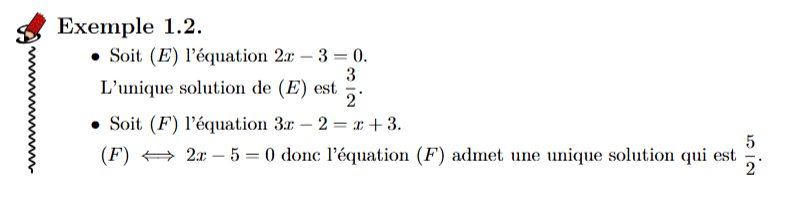
Résoudre une équation du premier degré
\(ax+b=0\)
avec (\(a\neq 0)\)

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

\text{Soit (E) l'équation }(2x+3)(3x-1)=0.\text{ On a : } \\ \begin{array}{cccc} & (E)\\ \iff& (2x+3)(3x-1)=0\\ \iff& (2x+3)=0 &\text{ ou }&(3x-1)=0\\ \iff& 2x=-3 &\text{ ou }&3x=1\\ \iff& x=-\dfrac{3}{2} &\text{ ou }&x=\dfrac{1}{3}\\ \end{array}
\text{L'ensemble des solution de (E) est :} \\ \{-\dfrac{3}{2};\dfrac{1}{3}\}

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

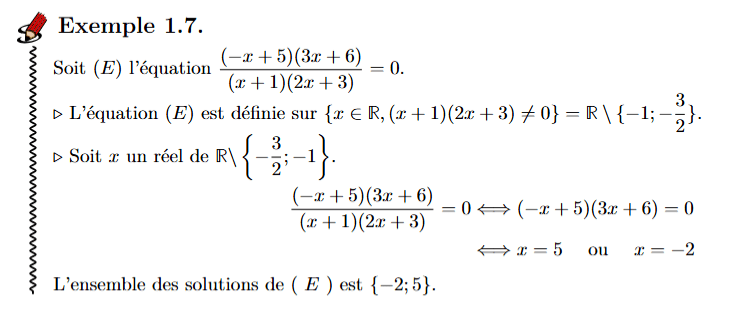
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une équation du second degré
\(ax^2+bx+c=0\)
avec (\(a\neq 0)\)

1. Si on reconnait une
identité remarquable ?

\begin{array}{cccc} &4x^2+20x+25&=&0\\ \iff&(2x+5)^2&=&0\\ \iff&(2x+5)&=&0\\ \iff&2x&=&-5\\ \iff&x&=&-\frac{5}{2} \end{array} \\\\\\ \text{L'ensemble des solutions est :}\\ \{-\frac{5}{2}\}

Exemple 1

Exemple 2

\begin{array}{cccccccc} &49-64t^2&=&0&&&&\\ \iff&(7-8t)(7+8t)&=&0&&&&\\ \iff&(7-8t)&=&0&\text{ ou }&(7+8t)&=&0\\ \iff&7&=&8t&\text{ ou }&8t&=&-7\\ \iff&t&=&\dfrac{7}{8}&\text{ ou }&8t&=&-\dfrac{7}{8}\\ \end{array}\\ \text{L'ensemble des solutions est } \{-\dfrac{7}{8}; \dfrac{7}{8} \}

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une équation du second degré
\(ax^2+bx+c=0\)
avec (\(a\neq 0)\)

2. Si on reconnait une
forme \(x^2-Sx+P\) 

Exemple 3

\begin{array}{cccccccc} &x^2-15x+56&=&0&&&&\\ \iff&(x-7)(x-8)&=&0&\text{ on a remarqué :}& S=7+8=15& P=7\times 8=56&\\ \end{array}\\ \text{L'ensemble des solutions est } \{7;8 \}

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une équation du second degré
\(ax^2+bx+c=0\)
avec (\(a\neq 0)\)

3. Méthode génerale

  1. On calcule le discriminant \(\Delta=b^2-4ac\).
2.\left\{ \begin{array}{cllcc} \text{Si }\Delta <0,&\text{il n'y a pas de solutions réelles.}&&& \\ \text{Si }\Delta =0,&\text{il y a une solution unique réelle:} & x_0=-\dfrac{b}{2a}&&\\ \text{Si }\Delta >0,&\text{il y a deux solutions réelles:} & x_1=\dfrac{-b+\sqrt{\Delta}}{2a} &\text{ et }& x_2=\dfrac{-b+\sqrt{\Delta}}{2a}\\ \end{array} \right.

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une équation du second degré
\(ax^2+bx+c=0\)
avec (\(a\neq 0)\)

3. Méthode génerale (exemples)

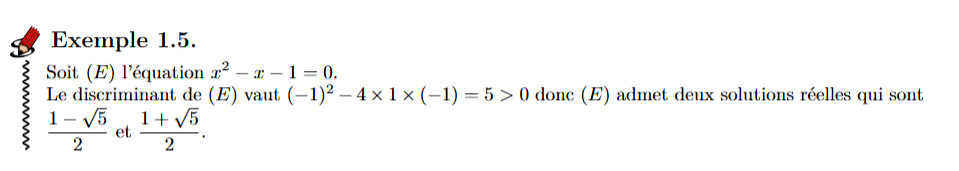
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une équation du second degré
\(ax^2+bx+c=0\)
avec (\(a\neq 0)\)

3. Méthode génerale (exemples)

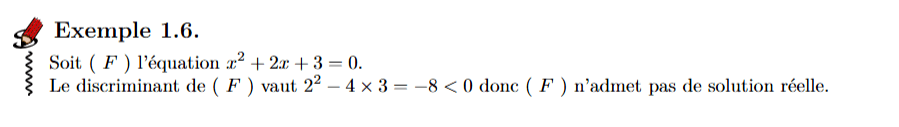
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une inéquation du premier degré

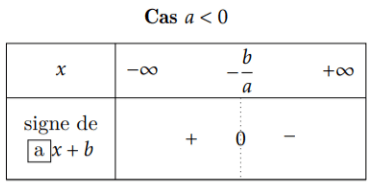
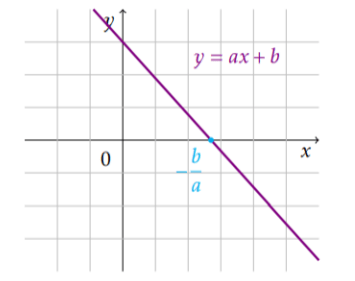
Méthode génerale: on étudie le signe de \(ax+b\)

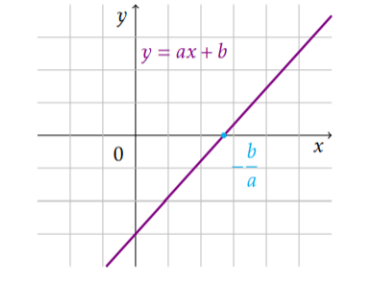
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une inéquation du premier degré

Méthode génerale: on étudie le signe de \(ax+b\)

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une inéquation du premier degré

\left[\dfrac{1}{3};+\infty\right[

L'ensemble des solutions est :

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

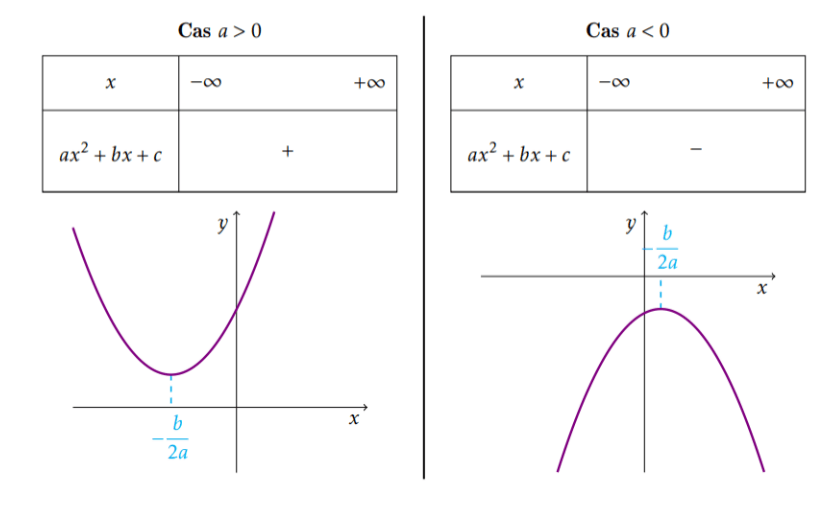
Rappel : La courbe de la fonction \( x\mapsto ax^2+bx+c\)
est une 

parabole

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Rappel : La courbe de la fonction \( f: x\mapsto ax^2+bx+c\)
est une 

parabole

Que la parabole soit convexe ou concave:
Les coordonnées de son "sommet"
sont (\(\alpha;\beta\))

  • \(\alpha=\)
  • \(\beta=\)
  • \(f(x)=ax^2+bx+c=\)

\(-\frac{b}{2a}\)

\(-\frac{\Delta}{4a}=f(\alpha)\)

\(a(x-\alpha)^2+\beta\)

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une inéquation du second degré

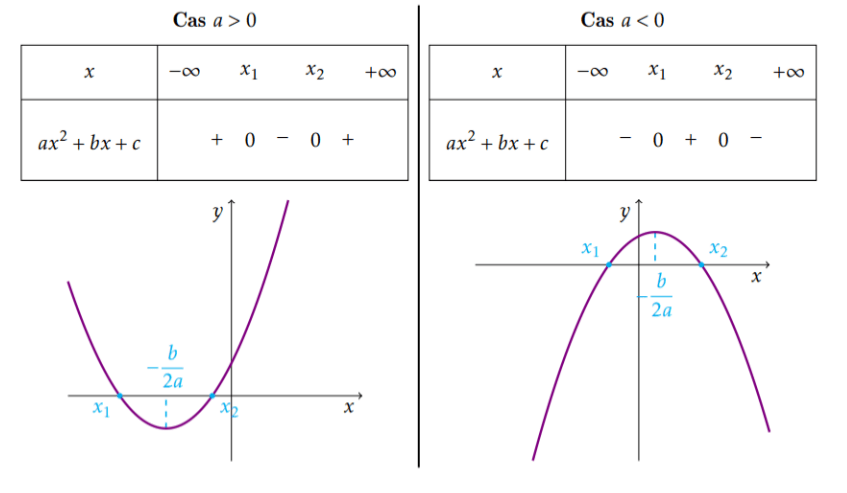
Méthode génerale: on étudie le signe de \(ax^2+bx+c\)

1. Cas où  \(\Delta=b^2-4ac >0\)

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une inéquation du second degré

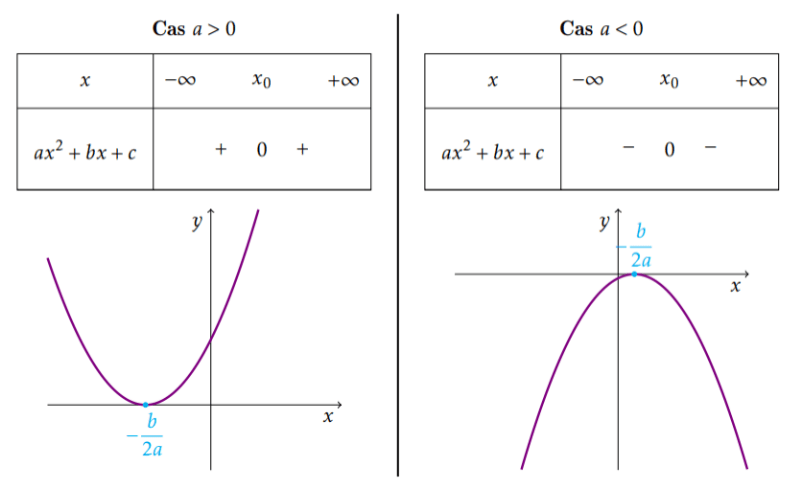
Méthode génerale: on étudie le signe de \(ax^2+bx+c\)

1. Cas où  \(\Delta=b^2-4ac=0\)

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une inéquation du second degré

Méthode génerale: on étudie le signe de \(ax^2+bx+c\)

1. Cas où  \(\Delta=b^2-4ac<0\)

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une inéquation du second degré

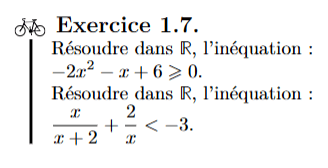
  • Calcul du discriminant: \(\Delta=(-1)^2-4\times(-2)\times(+6)=\)

49

  • Le trinôme \(-2x^2-x+6\)  a  donc 2 racines:
     
    \(x_1=\)                            \(x_2=\)
\dfrac{1-\sqrt{49}}{-4}=\dfrac{3}{2}
\dfrac{1+\sqrt{49}}{-4}=-2
  • \(a<0\)  donc l'ensemble des solutions est :
     
\left[-2;\dfrac{3}{2}\right]

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.2 Quelques règles indispensables

Résoudre une inéquation du second degré

Il s'agit de résoudre dans \(\R\setminus\{-2;0\}\) cette inéquation notée \( (E)\)

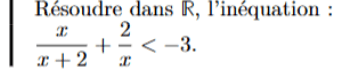
L'ensemble des solutions est:

]-2;0[\setminus \{-1\}


  \((E)\iff\dfrac{x}{x+2}+\dfrac{2}{x}+3<0\\\)
  \(\iff\dfrac{x\times x}{(x+2)x}+\dfrac{2(x+2)}{x(x+2)}+\dfrac{3x(x+2)}{x(x+2)}<0\\\)
 \(\iff\dfrac{4(x+1)^2}{(x+2)x}<0\)

 

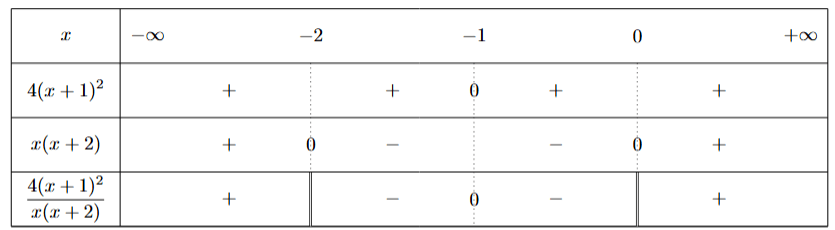
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Les quantificateurs

  • Le symbole « \(\forall\) » est un quantificateur universel  .
  • Le symbole « \(\exists\)» est un quantificateur existentiel.
  • Le  symbole « \(\exists !\)» est un quantificateur existentiel et d'unicité.

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Les quantificateurs

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Propositions (assertions)

Les propositions énoncées dans un cours sont VRAIES.

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

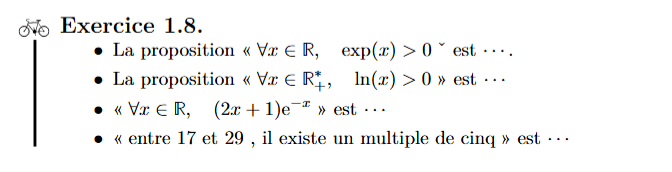
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

  • Soit F l'ensemble des filles d'une classe.
  • Soit G l'ensemble des garçons d'une classe.
  • Soit \(T(x)\) la taille en cm de l'individu \(x\) .

Que signifie les propositions suivantes :

\mathscr{P_1} : (\forall x\in F , \forall y\in G , T(x)< T(y) \quad)
\mathscr{P_2} :( \forall y\in G, \forall x\in F , T(x)< T(y) \quad)
\mathscr{P_3 } :(\exist x\in F , \exist y\in G , T(y)= T(x)+10 \quad)
\mathscr{P_4} : ( \exist y\in G , \exist x\in F , T(y)= T(x)+10 \quad )

Que constatez-vous?

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

  • Soit F l'ensemble des filles d'une classe.
  • Soit G l'ensemble des garçons d'une classe.
  • Soit \(T(x)\) la taille en cm de l'individu \(x\) .

Que signifie :

\mathscr{P_5} : (\forall y\in G , \exist x\in F , T(x)= T(y) \quad)
\mathscr{P_6} : ( \exist x\in F , \forall y\in G , T(x)= T(y) \quad)

Que constatez-vous?

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Connecteurs logiques

On considère deux propositions
 \(\mathcal{P}\) et   \(\mathcal{Q}\)

Le connecteur "ET"

La proposition \(\mathcal{P} \text { et } \mathcal{Q} \)
est la proposition qui est vraie lorsque :
les propositions \(\mathcal{P} \text { et } \mathcal{Q} \) sont  vraies simultanément

Pour un dé lancé, on considère :
\(\mathcal{P}\) : « le numéro sorti est pair »
\(\mathcal{Q}\) : «le numéro sorti est supérieur ou égal à 3 »

La proposition \(\mathcal{P} \text { et } \mathcal{Q} \) est la proposition :

 «                                                         »

le numéro sorti est 4 ou 6

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Connecteurs logiques

On considère deux propositions
 \(\mathcal{P}\) et   \(\mathcal{Q}\)

Le connecteur "OU"

La proposition \(\mathcal{P} \text { ou } \mathcal{Q} \)
est la proposition qui est vraie lorsque :
au moins l'une des deux propositions  est  vraies

Pour un dé lancé, on considère :
\(\mathcal{P}\) : « le numéro sorti est pair »
\(\mathcal{Q}\) : «le numéro sorti est supérieur ou égal à 3 »

La proposition \(\mathcal{P} \text { ou } \mathcal{Q} \) est la proposition :

 «                                                         »

le numéro sorti est 2,34,5 ou 6

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Connecteurs logiques

On considère deux propositions
 \(\mathcal{P}\) et   \(\mathcal{Q}\)

Le connecteur "\( \Rightarrow \)"

La proposition \(\mathcal{P} \Rightarrow  \mathcal{Q} \)
est la proposition qui est vraie lorsque :
si  \(\mathcal{P}  \)  est vraie alors \(\mathcal{Q}  \)   est  vraie

Pour un dé lancé, on considère :
\(\mathcal{P}\) : « le numéro sorti est pair »
\(\mathcal{Q}\) : «le numéro sorti est supérieur ou égal à 3 »

La proposition \(\mathcal{P} \Rightarrow  \mathcal{Q} \) est   la proposition:

 «                                                                                                              »

Si le numéro sorti est pair alors il est supérieur ou égal à 3

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Connecteurs logiques

On considère deux propositions
 \(\mathcal{P}\) et   \(\mathcal{Q}\)

La réciproque de la proposition \(\mathcal{P} \Rightarrow  \mathcal{Q} \)
est la proposition  \(\mathcal{Q} \Rightarrow  \mathcal{P} \)

Pour un dé lancé, on considère :
\(\mathcal{P}\) : « le numéro sorti est pair »
\(\mathcal{Q}\) : «le numéro sorti est supérieur ou égal à 3 »

La proposition réciproque de  \(\mathcal{P} \Rightarrow  \mathcal{Q} \) est   la proposition:

 «                                                                                                              »

Si le numéro sorti est supérieur ou égal à 3 alors il est  pair

Réciproque

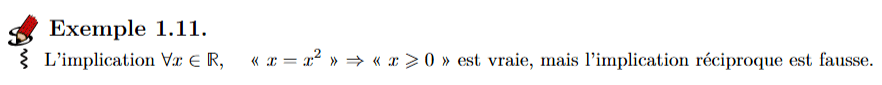
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Connecteurs logiques

On considère deux propositions
 \(\mathcal{P}\) et   \(\mathcal{Q}\)

Pour un dé lancé, on considère :
\(\mathcal{P}\) : « le numéro sorti est pair »
\(\mathcal{Q}\) : «le numéro sorti est supérieur ou égal à 3 »

La proposition  \(\mathcal{P} \iff \mathcal{Q} \) est   la proposition:

 «                                                                                                                     »  

 Le numéro sorti est supérieur ou égal à 3 
SI ET SEULEMENT SI  il est  pair

Le connecteur "\( \iff \)"

La proposition \(\mathcal{P} \iff  \mathcal{Q} \)
est la proposition qui est vraie lorsque :
les propositions  (\(\mathcal{P} \Rightarrow  \mathcal{Q} \) ) et ( \(\mathcal{Q} \Rightarrow  \mathcal{P} \)) sont simultanément vraies.

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Connecteurs logiques

On considère deux propositions
 \(\mathcal{P}\) et   \(\mathcal{Q}\)

Pour un dé lancé, on considère :
\(\mathcal{P}\) : « le numéro sorti est pair »
\(\mathcal{Q}\) : «le numéro sorti est supérieur ou égal à 3 »

La négation de la
proposition \(\mathcal{P} \) est  :
 

 non(\(\mathcal{P} \)) : 

 « Le numéro sorti est impair»

La négation "non"

La proposition non(\(\mathcal{P} \))
est la proposition contraire à  \(\mathcal{P} \) .

La négation de la
proposition \(\mathcal{Q} \) est  :
 

 non(\(\mathcal{Q} \)) : 

 « Le numéro sorti est  0 ou 1»

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Condition nécessaire/ Condition suffisante

  • si  la proposition                                est vraie.

Condition  suffisante
​pour avoir \(\mathcal{Q} \)

Condition  nécessaire
​pour avoir  \(\mathcal{P} \)

 \(\mathcal{P}  \) 

 \( \Rightarrow   \) 

 \(\mathcal{Q}  \) 

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Condition nécessaire/ Condition suffisante


  •  \(\ldots \Rightarrow \ldots  \)  
  •  \(\ldots \Rightarrow \ldots  \) 
  •  \(\ldots \Rightarrow \ldots  \) 


  • "Avoir son bac" est la condition
  • "Avoir  un frère" est la condition
  • "Avoir  le droite de vote " est la condition

nécessaire

suffisante

suffisante

\( \mathcal{P} \)  

\( \mathcal{Q} \)  

\( \mathcal{P} \)  

\( \mathcal{Q} \)  

\( \mathcal{P} \)  

\( \mathcal{Q} \)  

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Condition nécessaire/ Condition suffisante

x\in\{-3;3\}
x\in ]-\infty ,-3[\cup ]3;+\infty[

\(AB^2+AC^2=BC^2\)

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

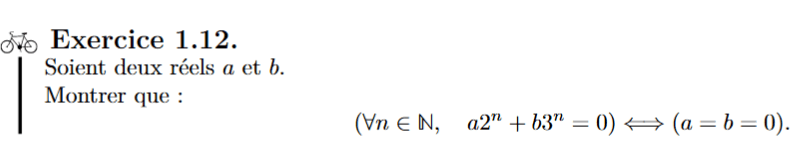
Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

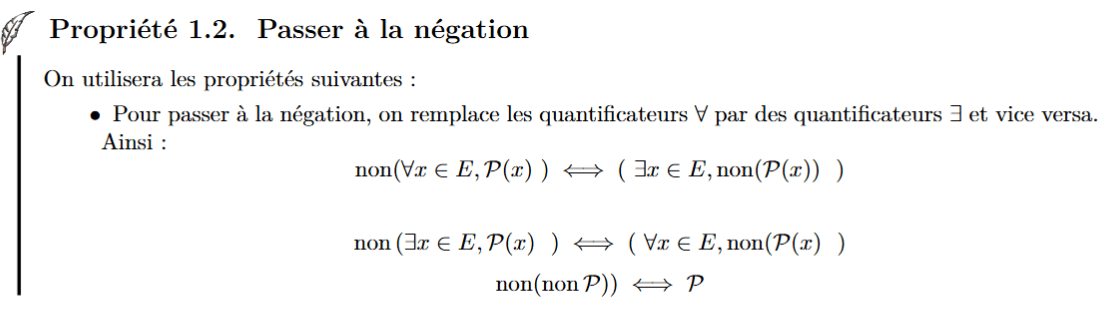
La négation de :" Tous les garçons de la classe ont une Livret A"

est :

"Il existe des garçons de la classe qui n'ont pas de Livret A"

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

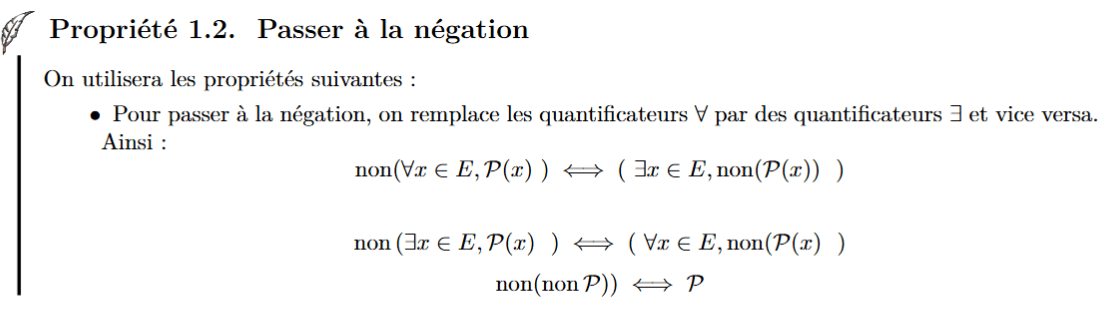
La négation de :"Il existe une fille de la classe qui  a le permis de conduire"

est :

"Toutes les  filles de la classe  n'ont pas de permis de conduire"

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

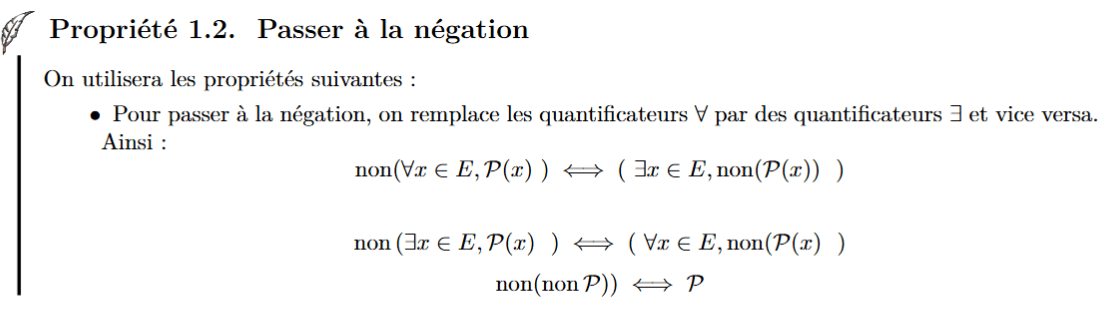
La négation de :"Pour  tout étudiant, il existe une  lettre de l'alphabet tel que cet étudiant possède un nom qui commence par cette  lettre"

est :

"Il existe un étudiant tel que pour toute lettre de l'alphabet , cet étudiant possède un nom qui ne commence pas par cette lettre."
 

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Table de vérité

Soient P et Q deux propositions

Rappel:

  • (P et Q) est vraie et seulement  si P et Q sont simultanément vraies
  • (P ou Q) est vraie et seulement  si au moins l'une des deux est vraie
P Q  non( P) non(Q) P et Q P ou Q non
(Pet Q)		 non
(P ou Q)		  non (P)
et
non (Q)   		 non(P)
ou
non(Q)
V V
V F
F V
F F

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Table de vérité

Soient P et Q deux propositions

non (P et Q) \(\iff\) non(P) ou non(Q)

non (P ou Q) \(\iff\) non(P) et non(Q)

P Q  non( P) non(Q) P et Q P ou Q non
(Pet Q)		 non
(P ou Q)		  non (P)
et
non (Q)   		 non(P)
ou
non(Q)
V V F F V V F F F F
V F F V F V V F F V
F V V F F V V F F V
F F V V F F V V V V

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Effet de la négation

\(\forall\)

\(\exists\)

et

ou

\(\mathcal{P}\)

\(\exists\)

\(\forall\)

et

ou

non(\(\mathcal{P}\))

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

 Supposons que  (  \(\mathcal{P}\)  \( \Rightarrow\) \(\mathcal{Q}\) ) est vraie.
Montrons que  ( non (\(\mathcal{Q}\))  \( \Rightarrow\)  non( \(\mathcal{P}\) ) ) est vraie.

On suppose que  non(\(\mathcal{Q}\)) est vraie

Si non(\(\mathcal{Q}\)) est vraie
alors \(\mathcal{Q}\) est fausse
alors \(\mathcal{P}\) est fausse (sinon contradiction)

alors non( \(\mathcal{P}\)) est vraie

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

 Supposons que ( non (\(\mathcal{Q}\))  \( \Rightarrow\)  non( \(\mathcal{P}\) ) ) est vraie.
Montrons que   (  \(\mathcal{P}\)  \( \Rightarrow\) \(\mathcal{Q}\) ) est vraie.

On suppose que  non(\(\mathcal{Q}\)) est vraie

Si  \(\mathcal{P}\) est vraie
alors  non(\(\mathcal{P}\)) est fausse
alors non(\(\mathcal{Q}\)) est fausse (sinon contradiction)

alors  \(\mathcal{Q}\) est vraie

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Réciproque et contrapposée "célèbres"

Il y a un sommet possédant
un angle droit

Le carré de la longueur du plus grand côté est égal à la somme des carrées des longueurs des deux autres côtés.

Soit un triangle dans
le plan euclidien.

Théorème de Pythagore

Sa réciproque

\(\mathcal{P}\)

\(\mathcal{Q}\)

  •  (  \(\mathcal{P}\)  \( \Rightarrow\) \(\mathcal{Q}\) ) est le théorème de Pythagore.
  •  (  \(\mathcal{Q}\)  \( \Rightarrow\) \(\mathcal{P}\) ) est la réciproque du théorème de Pythagore.
  • ( non (\(\mathcal{Q}\))  \( \Rightarrow\) non(\(\mathcal{P}\) ) ) est la contrapposée théorème de Pythagore. 

"Si le carré de la longueur du plus grand côté n'est pas égal à la somme des carrées des longueurs des deux autres côtés alors le triangle n'est pas rectangle."

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique





  • ...

Séquence 1: Rappels de calculs algébriques. Éléments de logique.

1.3 Eléments de logique

....

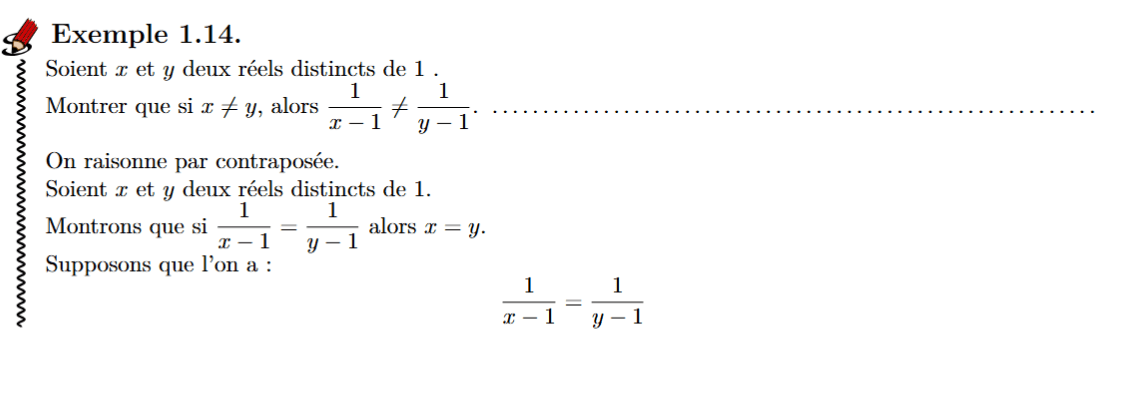
SEQUENCE 1

By intermaths.info

SEQUENCE 1

  • 87

More from intermaths.info