TD
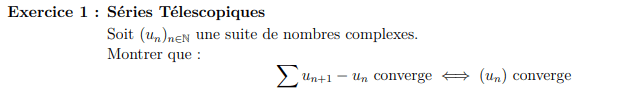
Somme partielle:
- \( S_n=\displaystyle\sum_{k=0}^n \left(u_{k+1}-u_k \right)\)
elle est télescopique
- \( S_n=u_{n+1}-u_0 \)
- Donc \( (S_n)_{n\in\N}\) converge \(\iff\) \( (u_n)_{n\in\N}\) converge

(a) Série géométrique de raison
\(q=e^{-3}\in]0;1[\) :
(b) Série téléscopique :
(c) Série téléscopique :
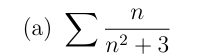
Soit \(u_n=\dfrac{n}{n^2+3}\) pour \(n\in \N\)
\(u_n\) est positif et \(u_n\underset{+\infty}{\sim} \dfrac{1}{n}\)
\(\sum\dfrac{1}{n}\) diverge donc \(\sum u_n\) diverge
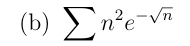
Soit \(u_n=\dfrac{n}{n^2+3}\) pour \(n\in \N\)
Soit \(u_n=n^2e^{-\sqrt{n}}\)pour \(n\in \N\)
D'après le théorème d'équivalence des séries à termes positifs
D'après les règles de Riemann
par croissances comparées
2>1 donc \(\sum u_n\) converge
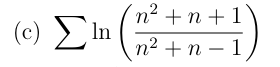
Soit, pour \(n\in \N\) ,
Or \( \ln(1+x) \underset{0}{\sim}x \)
D'après les règles de Riemann
par combinaison linéaire
\(\sum\dfrac{1}{n^2}\) converge donc \(\sum u_n\) converge
Encore des séries à termes positifs
Soit \(u_n=\dfrac{n!}{e^{2n}}\) pour \(n\in \N\)
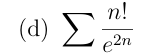
\( \dfrac{u_{n+1}}{u_n}=\dfrac{(n+1)!}{e^{2(n+1)}} \dfrac{e^{2n}}{n!}=\dfrac{n+1}{e^2} \underset{n\to +\infty}{\to} +\infty \)
D'après la règle de D'Alembert
\(\sum u_n\) diverge
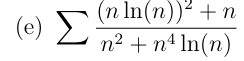
Soit \(u_n=\dfrac{(n\ln(n))^2+n}{n^2+n^4\ln(n)}\) pour \(n\in \N\setminus\{0;1\}\)
- \((n\ln(n))^2+n\underset{+\infty}{\sim} (n\ln(n))^2\)
- \( n^2+n^4\ln(n)\underset{+\infty}{\sim} (n^4\ln(n))\)
donc
\( n^{\frac{3}{2}}u_n\underset{+\infty}{\sim} \dfrac{\ln(n)}{n^\frac{1}{2}}\)
\(u_n\underset{+\infty}{\sim} \dfrac{\ln(n)}{n^2} \)
or
\( n^2= n^\frac{3}{2} n^\frac{1}{2} \)
donc
donc
par croissances comparées
\(\frac{3}{2}\)>1 donc \(\sum u_n\) converge
D'après les règles de Riemann
Soit \(u_n=\dfrac{n!}{e^{2n}}\) pour \(n\in \N\)
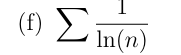
Soit \(u_n=\dfrac{1}{\ln(n)}\) pour \(n\in \N\setminus\{0;1\}\)
par croissances comparées
\(\frac{1}{2}\)<1 donc \(\sum u_n\) diverge
D'après les règles de Riemann
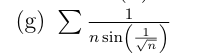
Soit \(u_n=\dfrac{1}{n\sin(\frac{1}{\sqrt{n}})}\) pour \(n\in \N\setminus\{0\}\)
\( \sin(x) \underset{0}{\sim}x \)
donc \( \sin(\frac{1}{\sqrt{n}} ) \underset{+\infty}{\sim}\frac{1}{\sqrt{n}}\)
\( n\sin(\frac{1}{\sqrt{n}} ) \underset{+\infty}{\sim}n\frac{1}{\sqrt{n}}\)
\( n\sin(\frac{1}{\sqrt{n}} ) \underset{+\infty}{\sim}n\frac{1}{\sqrt{n}}\)
\( \dfrac{1}{n\sin(\frac{1}{\sqrt{n}} )} \underset{+\infty}{\sim}\dfrac{1}{n^{\frac{1}{2}}}\)
\(\sum\dfrac{1}{n^\frac{1}{2}}\) est une série de Riemann divergente
donc \(\sum u_n\) diverge
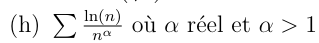
Soit \(u_n=\dfrac{\ln(n)}{n^\alpha}\) pour \(n\in \N\setminus\{0\}\)
par croissances comparées
donc \(\sum u_n\) converge
D'après les règles de Riemann
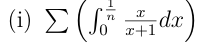
Soit \(u_n=\displaystyle\int_0^\frac{1}{n}\dfrac{x}{x+1} dx\) pour \(n\in \N\setminus\{0\}\)
\(u_n=\displaystyle\int_0^\frac{1}{n}\dfrac{x+1-1}{x+1} dx\)
On a:
par combinaison linéaire
\(\sum\dfrac{1}{n^2}\) converge donc \(\sum u_n\) converge

Soit \(n\in\N^*\),
les termes sont strictement positifs


Si \(\alpha +\frac{1}{2}\neq 0\) :
Si \(\alpha +\frac{1}{2}= 0\) :
(b)
Si \(\alpha +\frac{1}{2}\neq 0\) :
Si \(\alpha +\frac{1}{2}= 0\) :
\(\sum v_n\) diverge
\(\sum v_n\) converge

Si \(\alpha =- \frac{1}{2}\) :
(c)
\(\sum v_n= \sum \left(\ln(u_{n+1}-\ln(u_n) \right)\)
série téléscopique
Ainsi : \(\left(\ln(u_{n}) \right)_n\) converge vers \(\ell\)
La continuité de la fonction exponentielle implique : \(\left(u_{n} \right)_n\) converge vers \(e^\ell\)>0
James Stirling montre que \(e^\ell=\sqrt{2\pi}\) et crée la formule

(a)
\( \sum u_n \) converge \( \Rightarrow \lim\limits_n u_n =0\)
Donc :
Ainsi \( \sum v_n \) converge
\( \sum v_n \) converge \( \Rightarrow \lim\limits_n v_n =0\)
(b)
Donc :
Ainsi \( \sum u_n \) converge
- Rappel: \( \forall x\in\R_+, \sin(x)\leqslant x\)
Donc
Remarque:
la suite est bien définie car \([0;\frac{\pi}{2}]\) est stable par \(f\)
- La fonction sinus est
strictement croissante sur \([0,\frac{\pi}{2} ]\)
(a)
\(f\) est continue donc \(f(\ell)=\ell\) donc \(\ell=0\)
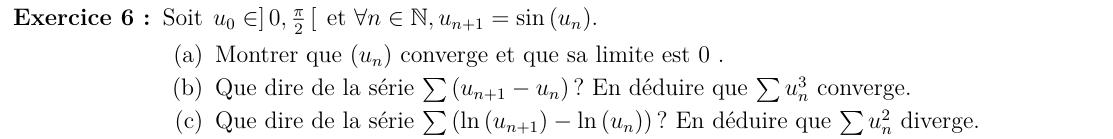
(b)
\(\sum (u_{n+1}-u_n)\) et \(\ (u_n)_n\) sont de même nature
donc \(\sum (u_{n+1}-u_n)\) converge
On sait que: \(sin(x)\underset{0}{=} x-\dfrac{x^3}{3!}+o(x^3)\)
\(u_n\underset{n\to+\infty}{\to}0\) donc \(sin(u_n)\underset{+\infty}{=} u_n-\dfrac{u_n^3}{6}+o(u_n^3)\)
\(\iff u_{ n+1}-u_n\underset{+\infty}{=}-\dfrac{u_n^3}{6}+o(u_n^3)\)
\(\iff 6( u_n-u_{ n+1})\underset{+\infty}{\sim}u_n^3\)
\(\sum (u_n-u_{n+1})\) et \(\sum u_n^3\) sont de même nature
Donc, \(\sum u_n^3\) est convergente
(c)
On sait que: \(\dfrac{sin(x)}{x}\underset{0}{=} 1-\dfrac{x^2}{3!}+o(x^2)\)
\(\sum (\ln(u_n)-\ln(u_{n+1}))\) et \(\sum u_n^2\) sont de même nature
Donc, \(\sum u_n^3\) est convergente
Et: \(\ln(1-x)\underset{0}{=} -x-\dfrac{x^2}{2}+o(x^2)\)
Donc :
Rappel :
Il faut un DL au même ordre
!!
\(\sum (\ln(u_{n+1})-\ln(u_n))\) et \(\ (\ln(u_n))_n\) sont de même nature
Or, \(\lim\limits_n \ln(u_n) =-\infty\)
donc \(\sum (\ln(u_{n+1})-\ln(u_n))\) diverge
donc \(\sum u_n^2\) diverge
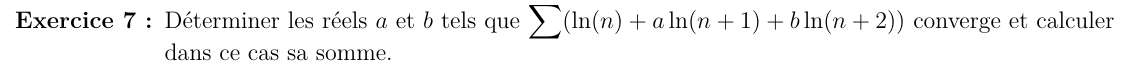
Soit
\(u_n=\ln(n)+a\ln(n+1)+b\ln(n+2)\) pour \(n\in \N\setminus\{0\}\)
Si \(1+a+b\neq 0\) :
\(\lim\limits_n u_n =\pm\infty\)
\(\sum u_n\) diverge grossièrement
Si \(1+a+b=0\) :
Si \(a+2b\neq0\) :
\( u_n \underset{+\infty}{\sim} (a+2b)\dfrac{1}{n}\)
\(\sum u_n\) diverge
Si \(a+2b= 0\) :
\( u_n \underset{+\infty}{\sim} -(\dfrac{a}{2}+2b)\dfrac{1}{n^2}\)
\(\sum u_n\) converge
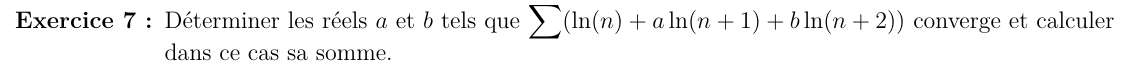
\(u_n=\ln(n)-2\ln(n+1)+\ln(n+2)\)
\(u_n=\ln(n)-\ln(n+1)-\ln(n+1)+\ln(n+2)\)
\(u_n=\ln(n)-\ln(n+1)-\left(\ln(n+1)-\ln(n+2)\right)\)
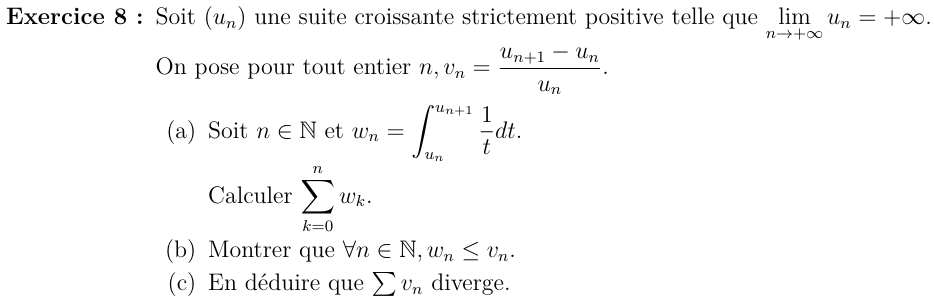
(a)
(b)
car :
\(\forall x>-1, ln(1+x)\leqslant x\)
et
\(\forall n\in\N,v_n>0\)
Pour tout entier \(n\)
(c)
D'après le théorème de comparaison des séries à termes positifs
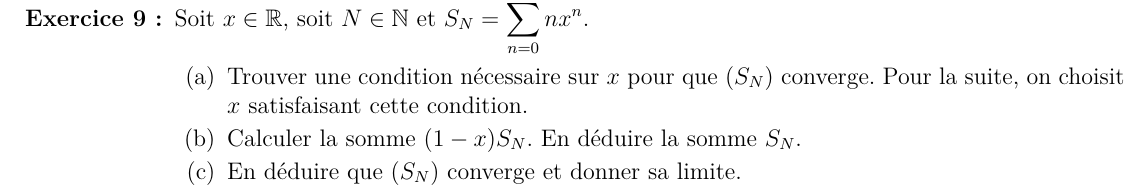
- \((S_n)_n\) converge implique :
\( \lim\limits_n nx^n=0 \)
(a)
(b)
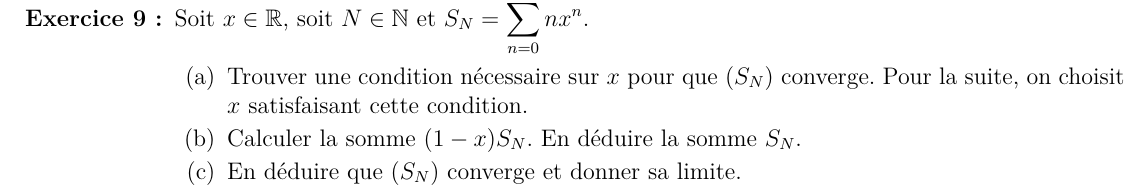
(c)
\( \lim\limits_n x^n=0 \) et
\(0<x<1\)
\( \lim\limits_n nx^n=0 \) donc
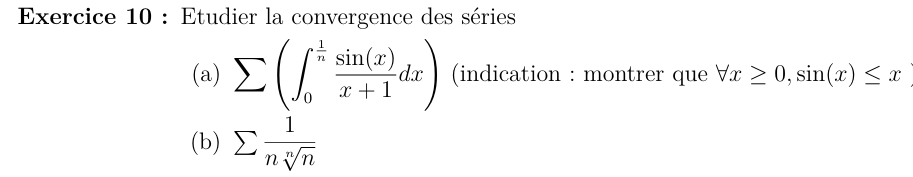
\( \underset{+\infty}{\sim} \dfrac{1}{2n^2}\)
(a)
(b)
\( \underset{+\infty}{\to} e^0\)

(a)
\( \underset{n\to+\infty}{\to}1\)

(b)
vu en cours

(c)
coup de pouce 1

(d)
coup de pouce 2
(e)
coup de pouce 3
preuve par récurrence
donc \( \lim\limits_n \displaystyle\prod_{k=1}^n \left(1+u_k\right) =+\infty\)
\( \underset{n\to+\infty}{\to}1\)

Approfondissement
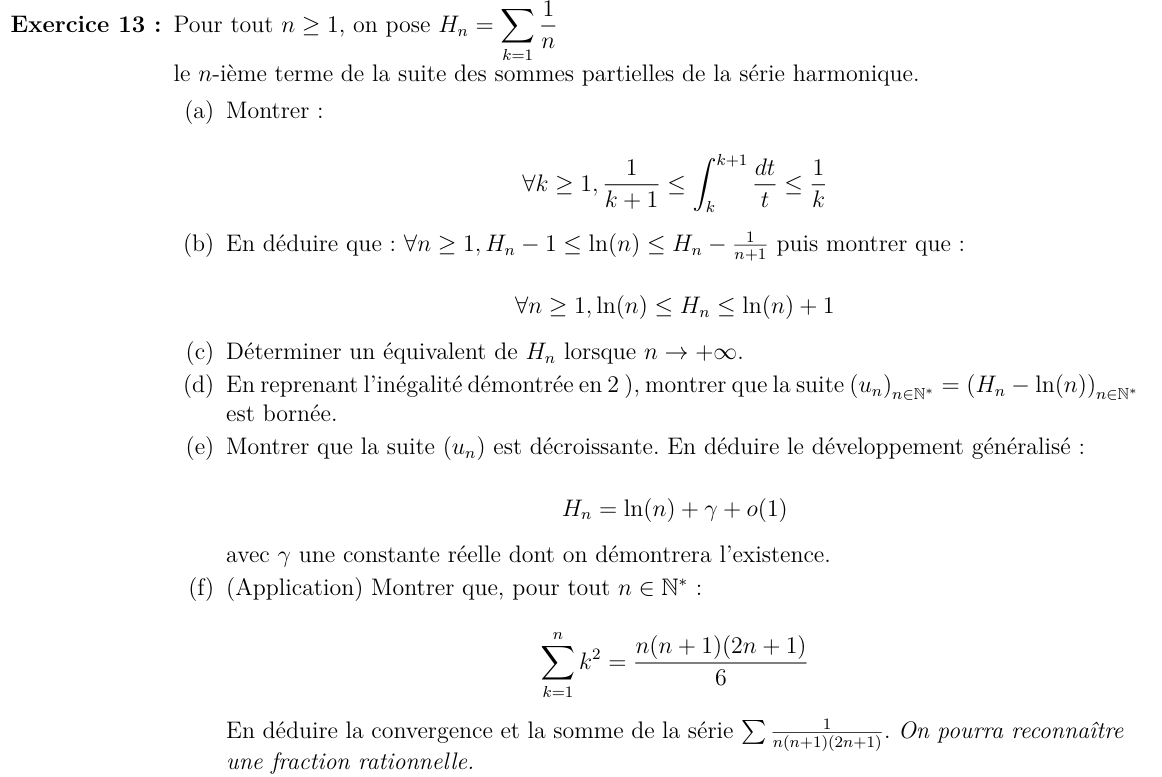
Approfondissement
TD
By intermaths.info
TD
- 42



