TD 2ème partie
Intégration

et ne s'annule pas sur I
}
Oops ! méthode imposée
Rappel:
Application avec :
\(\iff\)
D'après le c)
Soit \(x\in \R_+^*\)
Pour tout \(t \in [x,3x]\)
Donc
Conclusion
D'après le c)
Soit \(x\in \R_-^*\)
Pour tout \(t \in [3x,x]\)
Donc
Conclusion
Allons plus loin,
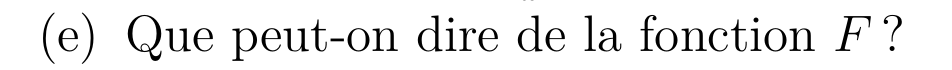
D'après le d)
\(F\) est donc continue \(\R\)
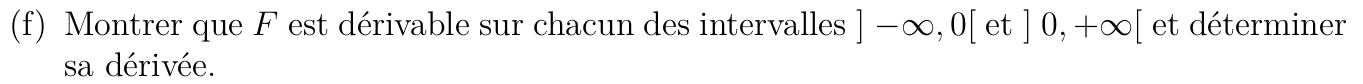
Dérivabilité sur \( ]0,+\infty[\)
Dérivabilité sur \(]-\infty,0[\)
Soit \(a_1\in \R_-^*\)
Soit \(a_2\in \R_+^*\)
\(\forall x\in \R_-^*\),
\(\forall x\in \R_+^*\),
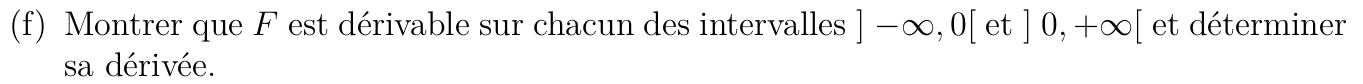
\(\forall x\in \R_-^*\),
\(\forall x\in \R_+^*\),
\(\forall x\in \R^*\),
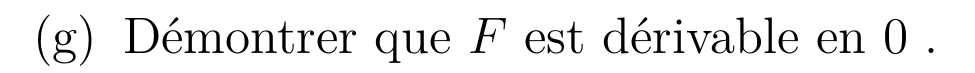
- \(F\) est continue sur \(\R\)
- \(F\) est dérivable sur \(\R^*\)
- Que peut -on dire de \(\lim \limits_{x\to 0} F'(x) \) ?
- \( \cos(3x)\underset{0}{=}1-\frac{9x}{2!} +o(x^2)\)
- \( \cos(x)\underset{0}{=}1-\frac{x^2}{2} +o(x^2)\)
- \( \cos(3x)-\cos(x)\underset{0}{=}-4x^2 +o(x^2)\)
- \( \dfrac{\cos(3x)-\cos(x)}{x}\underset{0}{=}-4x +o(x)\)
On a :
Donc :
D'après le théorème
de la limite de la dérivée :
\(F\) est dérivable en 0 et :
\(F'(0)=0\)
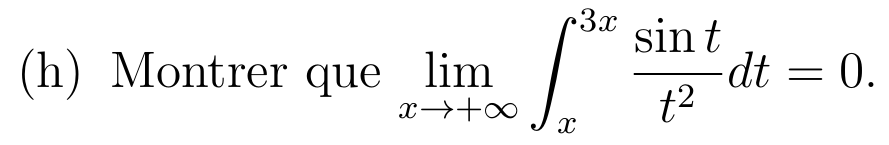
Soit \(x>0\)
On conclut grâce au théorème des gendarmes
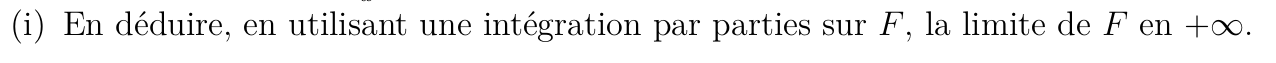
Soit \(x>0\)
On conclut grâce avec le h) et le théorème des gendarmes

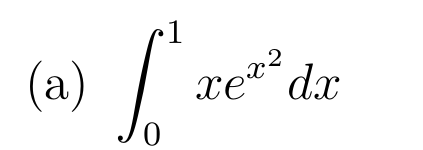
Soit \( u:x\mapsto x^2\) de classe \(\mathcal{C}^1\) sur \(\R\)
Primitive de référence

Soit \( u:x\mapsto x^2\) de classe \(\mathcal{C}^1\) sur \(\R\)
Primitive de référence
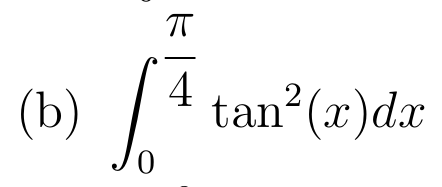

Soit \( u:x\mapsto \ln(x)\) de classe \(\mathcal{C}^1\) et ne s'annule pas sur \(]1;+\infty[\)
Primitive de référence
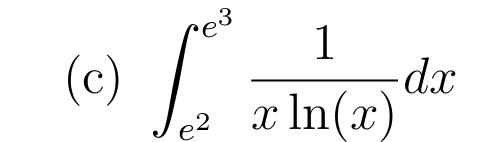

Soit \( u:x\mapsto 1+x\) de classe \(\mathcal{C}^1\) sur \([0;1]\)
Primitive de référence
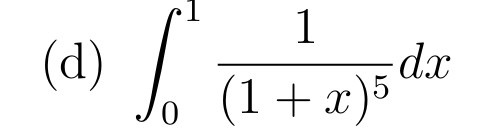

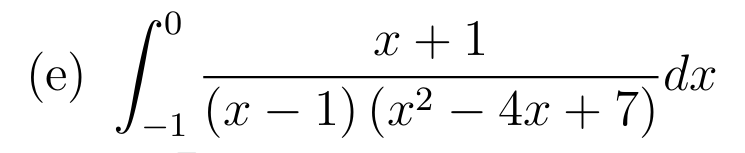

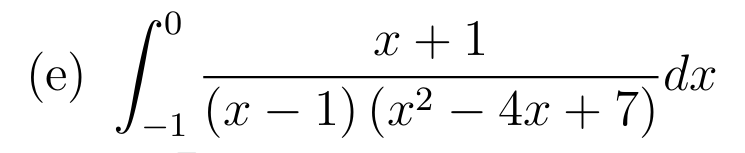

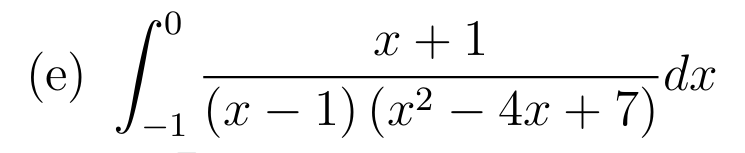
Changement de variable affine: \(t=x-2 \iff x=t+1 ,( dx=dt) \)

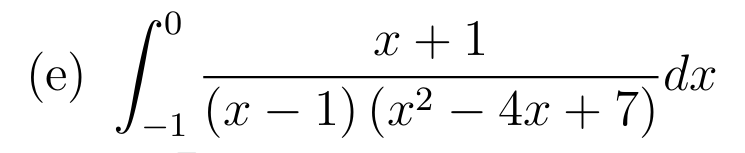
Changement de variable affine:

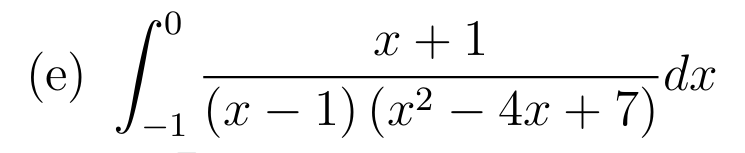
Rappel: \( \arctan(\sqrt{3}) =\dfrac{\pi}{ 3}\)

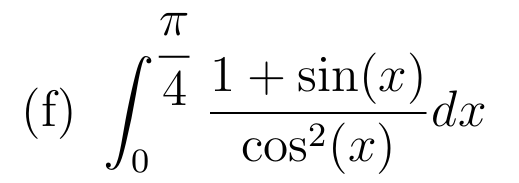
détail fait le lundi 02 en classe
=\(\sqrt{2}\)

détail fait le lundi 02 en classe
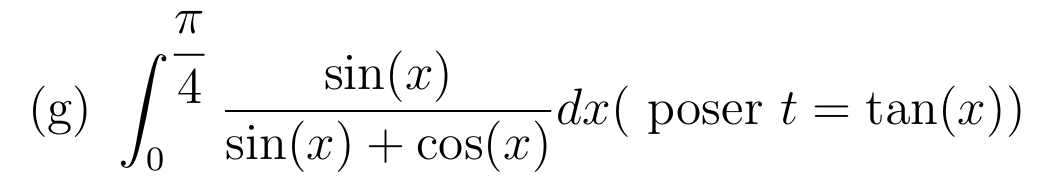
Changement de variable affine:
\(C\in\R\)
\( x\mapsto e^x\) est de classe \(C^1\) et bijective de \(\R \) sur \(]0;+\infty[\)
Changement de variable : \(t=e^x \iff x=\ln(t) , dx=\dfrac{dt}{t}\)
Pour \(x\in I\)
\(I=]-\infty;0[\) ou \(I=]0;+\infty[\)
Plus grands intervalles de validité
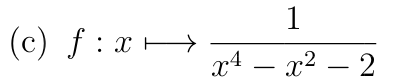
Pour \(x\in I\)
\(I=]-\infty;-\sqrt{2}[\) ou \(]-\sqrt{2};\sqrt{2}[\) ou \(I=]\sqrt{2};+\infty[\)
Plus grands intervalles de validité
\(I=\R\)
Plus grands intervalles de validité
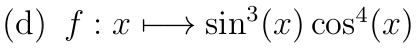
Soit \( u:x\mapsto \cos(x)\) de classe \(\mathcal{C}^1\) sur \(\R\)
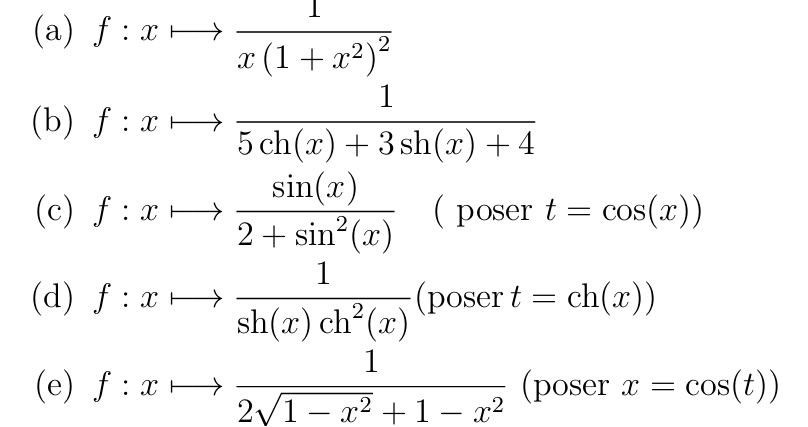
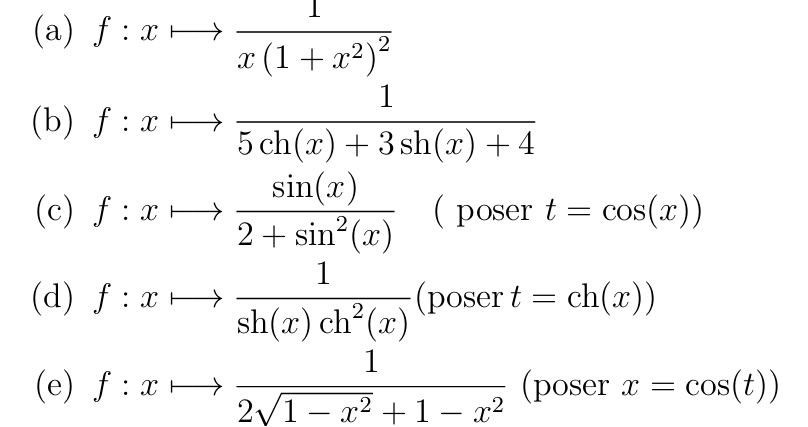
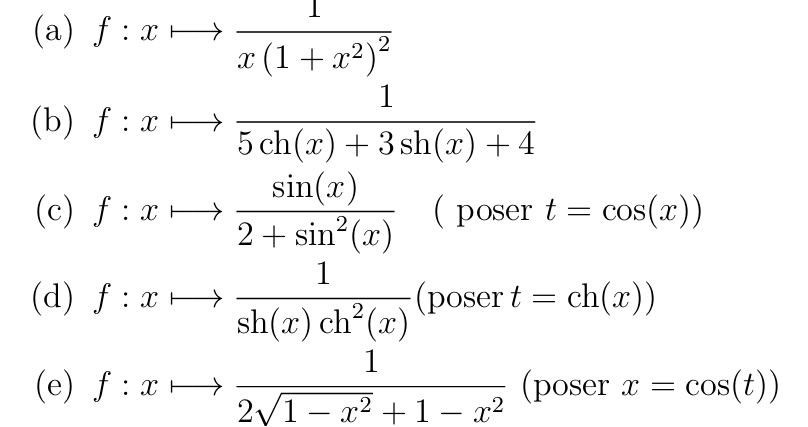
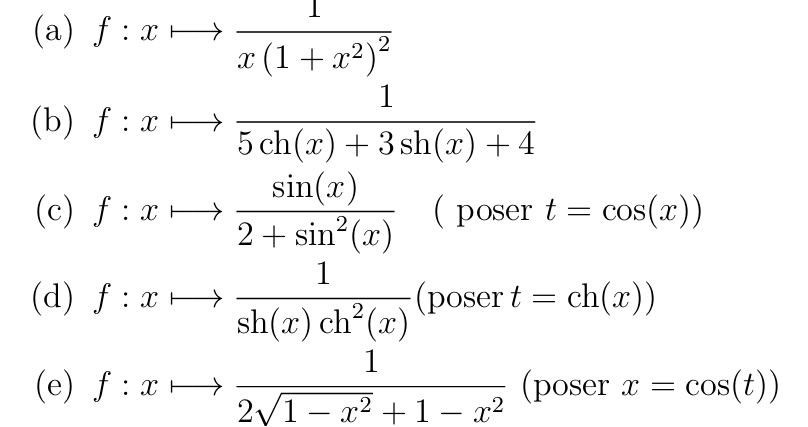
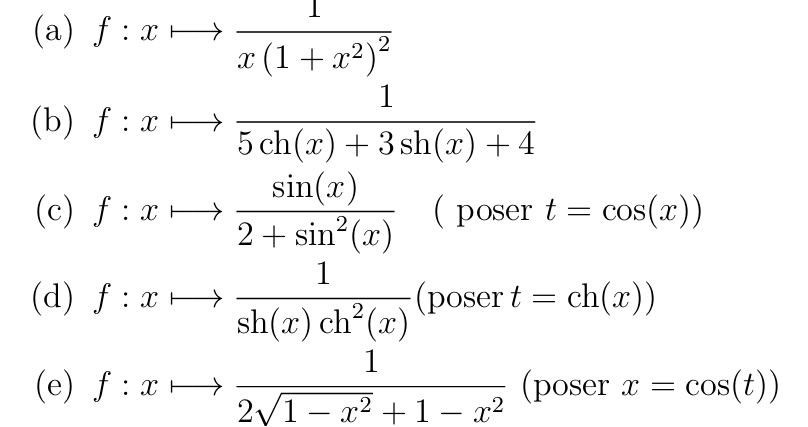
INTEGRATION_TD3
By intermaths.info
INTEGRATION_TD3
- 58



