Equation différentielle linéaire d'ordre 1
17/04/2024
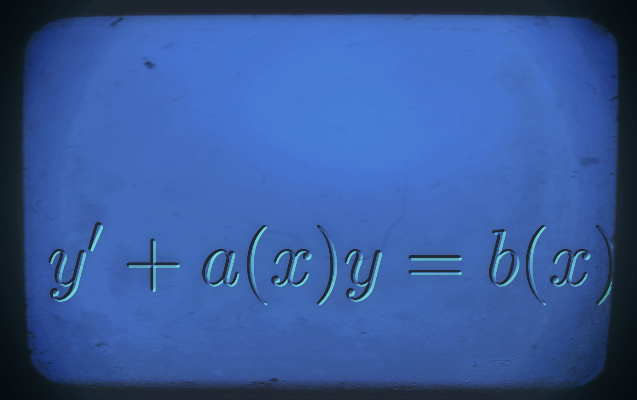
Equations différentielles linéaires d'ordre 1
ay'+by=c(t)
Equation différentielle linéaire d'ordre 1
à coefficients constants
a\neq 0
\iff y'+\dfrac{b}{a}~y=\dfrac{c(t)}{a}
coefficient constant
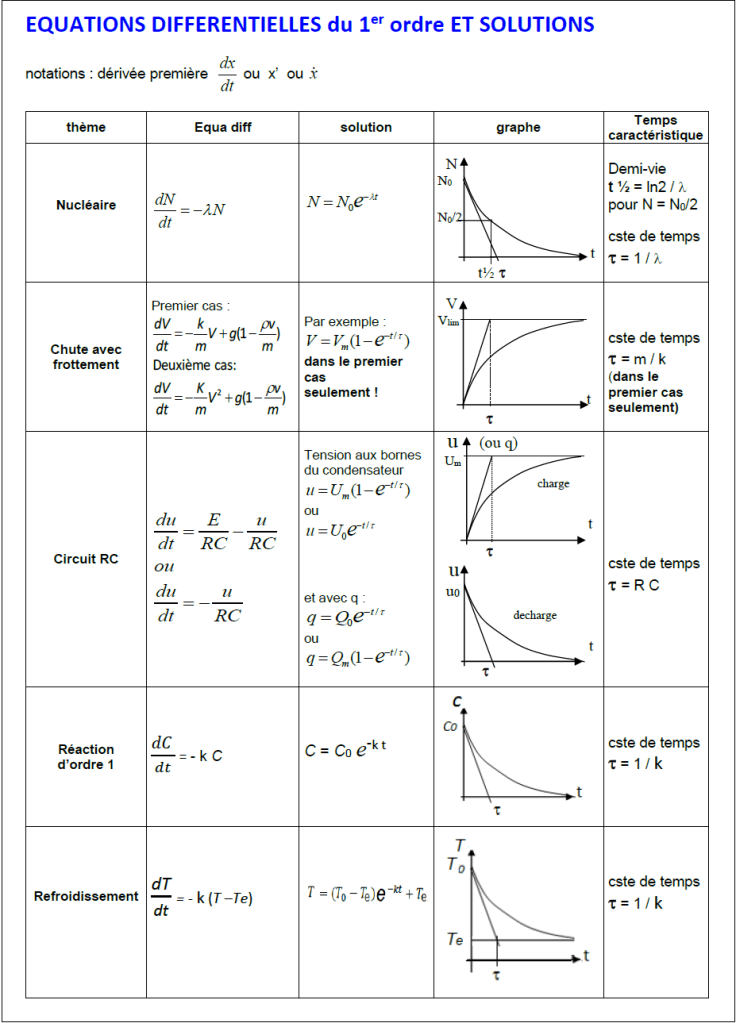
\( ay'+b y=0\)
Forme
\( y''+ay^2=b \)
\( ay'+b y=c \)
\( ay'+b y=0\)
\( ay'+b y=0\)
\( ay'+b y=0\)
Text
Coefficients a et b constants
\( ay'+b y=c \)
Equations différentielles linéaires d'ordre 1
Equations différentielles linéaires d'ordre 1
à coefficient constant
y'+a(t)~y=b(t)
fonction de \( t \)
Cas de coefficients a et b non constants
loi de Newton du refroidissement
échauffement d’un objet dans un environnement variable
Equation différentielle linéaire d'ordre 1
Equation différentielle linéaire d'ordre 1
1. (\(E_1)\) : voir chapitre correspondant
3. \( (E_3) : \text{non sous la forme } y'+a(x)=b(x) \)
2. \( (E_2) : y'+a(x)y=b(x) \)
avec \( x\mapsto \dfrac{x^2+1}{x}\) et \( x\mapsto \dfrac{e^x}{x} \) continues sur l'ouvert \(]0;+\infty[\)
Equation différentielle linéaire d'ordre 1
Autrement dit
\( S_H \) est
un sous-espace vectoriel de
\mathcal{F}(\mathbb{R},\mathbb{R})
Equation différentielle linéaire d'ordre 1
Mieux.
\( S_H \) est
un sous-espace vectoriel de
\mathcal{C}^1(\mathbb{R},\mathbb{R})
Equation différentielle linéaire d'ordre 1
I est un intervalle ouvert
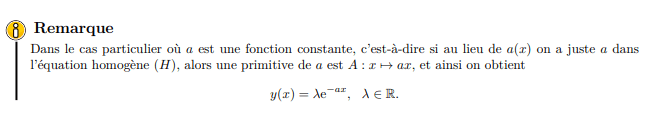
Equation différentielle linéaire d'ordre 1
a: x \mapsto
y'+a(x)y=0
A: x \mapsto
-x
\mathcal{S}_H=\left\{\begin{aligned} y_0: I & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{\frac{x^2}{2}} , \lambda\in \mathbb{R}\end{aligned}\right\}
a: x \mapsto
A: x \mapsto
\sin(x)
-\cos(x)
-\dfrac{x^2}{2}
\mathcal{S}_H=\left\{\begin{aligned} y_0: I & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{\cos(x)} , \lambda\in \mathbb{R}\end{aligned}\right\}
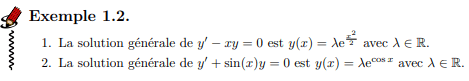
continue sur \( I=\mathbb{R}\)
continue sur \( I=\mathbb{R}\)
Equation différentielle linéaire d'ordre 1
(E) y'+a(x)y=b
Si \( a\) est constante et \( a\) est de la forme:
- \( x\mapsto P(x) \)
- \( x\mapsto P(x) e^{mx}\)
- \( x\mapsto A\cos(\omega x)+B\sin(\omega x) \)
}
Voir chapitre
où les
coefficients
sont constants
L'ensemble des solution de (E) est :
\mathcal{S}=\left\{\begin{aligned} y: I & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{-A(x)}+y_p , \lambda\in \mathbb{R}\end{aligned}\right\}
Equation différentielle linéaire d'ordre 1
(E) y'+a(x)y=b
Preuve : Existence de la fonction \( \lambda\) :
Soit \(x\mapsto b(x) e^{A(x)}\)
Cette fonction est définie sur I et est obtenue par produit et composition de fonctions continues donc elle est continue sur I
elle admet donc une primitive .
Soit \( \lambda \) une de ses primitives .
On considère \( y_p: x\mapsto \lambda (x) e^{-A(x)}\)
Equation différentielle linéaire d'ordre 1
(E) y'+a(x)y=b
Montrons que \(y_p\) est une solution de (E)
\forall x\in I, \quad (y_p)'(x)=\lambda'(x)e^{-A(x)}- \lambda(x) a(x)e^{-A(x)}
\( y_p: x\mapsto \lambda (x) e^{-A(x)}\)
=b(x)e^{A(x)}e^{-A(x)}- a(x) \lambda(x) e^{-A(x)}
=b(x)- a(x)y_p(x)
\text{Bilan: }\forall x\in I, \quad (y_p)'(x)+a(x)y_p(x)=b(x)
Preuve (suite): Existence de la fonction \( \lambda\) :
Equation différentielle linéaire d'ordre 1
Soit \( \mathcal{S}\) l'ensemble des solutions de : \( (E) : y'+a(x)y=b(x) \)
Soit \( y_p\) une solution particulière de \( (E) \), on montre que:
\mathcal{S}=\left\{\begin{aligned} y: I & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{-A(x)}+y_p, \lambda\in \mathbb{R}\end{aligned}\right\}
Soit \( y \in \mathcal{S}\) :
On vérifie aisément que \( y-y_p \) est une solution particulière de \( (H) \)
En effet, \( y'+a(x)y=b(x) \)
et, \( y_p'+a(x)y_p=b(x) \)
(on soustrait membre à membre )
\( y-y_p \) est une solution de \( (H) \)
\left\{\begin{aligned} y: I & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{-A(x)}+y_p, \lambda\in \mathbb{R}\end{aligned}\right\}\subset \mathcal{S}
Réciproquement soit :
On a:
Sur I,il existe \( \lambda \in \mathbb{R}\) tel que \(y=\lambda e^{-A(x)}+y_p \)
Ainsi, \( y'+a(x)y=-a(x)\lambda e^{-A(x)}+y_p' +a(x) (\lambda e^{-A(x)}+y_p)\)
= \( -a(x)\lambda e^{-A(x)}-a(x)y_p+b(x) +a(x) (\lambda e^{-A(x)}+y_p)\)
\( y-y_p \) est une solution particulière de \( (H) \)
ainsi
y-y_p\in \left\{\begin{aligned} y: I & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{-A(x)}, \lambda\in \mathbb{R}\end{aligned}\right\}
On a montré que:
y\in\left\{\begin{aligned} y: I & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{-A(x)}+y_p, \lambda\in \mathbb{R}\end{aligned}\right\}
= \( b(x)\)
On a montré que:
\mathcal{S}\subset \left\{\begin{aligned} y: I & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{-A(x)}+y_p, \lambda\in \mathbb{R}\end{aligned}\right\}
Equation différentielle linéaire d'ordre 1
L'ensemble des solutions de (\(H\)) est :
\mathcal{S}_H=\left\{\begin{aligned} y: \mathbb{R} & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{-x} , \lambda\in \mathbb{R}\end{aligned}\right\}
a: x \mapsto 1
b: x \mapsto \dfrac{1}{1+e^x}
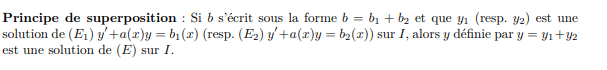
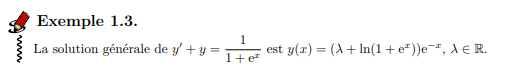
sont continues sur \(I=\mathbb{R}\)
Equation différentielle linéaire d'ordre 1
L' ensemble des solutions de (E) est :
\mathcal{S}=\left\{\begin{aligned} y: \mathbb{R} & \rightarrow \mathbb{R} \\ x & \mapsto \lambda e^{-x}+ln(1+e^x) e^{-x}, \lambda\in \mathbb{R}\end{aligned}\right\}
\forall x\in I ,y_p(x)= \lambda(x) e^{-x}
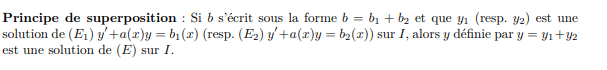
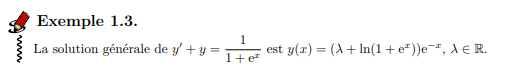
Solution particulière \(y_p\) :
\forall x\in I ,\lambda'(x)= b(x)e^{A(x)}
\text{.... la mémorisation accélère le processus , sinon on dérive } \lambda
= \dfrac{e^{x}}{1+e^x}
donc
\forall x\in I ,\lambda(x) = \ln(\vert 1+e^x \vert )= \ln( 1+e^x )
Equation différentielle linéaire d'ordre 1
\left\{\begin{aligned} y'+a(x)y=b(x) & ~~(E)\\ y(x_0)=y_0 & \text{ une condition initiale}\end{aligned}\right.
\(a\) et \(b\) sont continues sur un intervalle ouvert I
Soit( \(x_0,y_0) \in I \times \mathbb{R}\)
Problème de
Cauchy-Lipschitz
(E) ~~ y' +\dfrac{y}{e^{-x}-1}=\dfrac{1}{e^x-1}
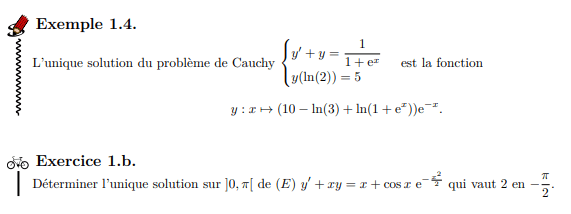
Résoudre l'équation différentielle suivante:
Equation différentielle linéaire d'ordre 1
Equation différentielle linéaire d'ordre 1
!!
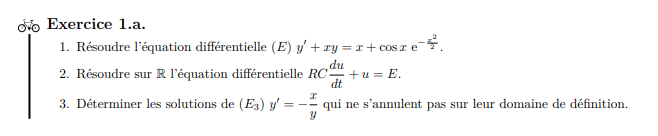
à faire
\((E_3)\\ \iff yy'=-x \\\iff \dfrac{1}{2}(y^2)'=-x \\ \iff (y^2)'=-2x\)
\(\iff y^2=-x^2+C\) avec C >0
\(\iff y=\sqrt{-x^2+C}\) sur \(I=]-\sqrt{C};\sqrt{C}[\)
\( y \) est dérivable sur I donc continue sur I, ainsi d' après la page précédente
à faire
\(\text{ ou } y=-\sqrt{-x^2+C}\) sur \(I=]-\sqrt{C};\sqrt{C}[\)
EDLO1
By intermaths.info
