TD (éléments de correction)
Démonstration:
S_n=\sum_{k=0}^{n } u_k
Pour tout \(n\in \N\),
u_n+S_{n-1}=u_n+\sum_{k=0}^{n-1 } u_k =+\sum_{k=0}^{n } u_k =S_n
Donc , pour tout \(n\in \N^*\),
Et , pour tout \(n\in \N^*\),
u_n=S_n-S_{n-1}
Démonstration :
Soit \( (S_n)_{n\in \N} \) la suite des sommes partielles de la suite \( (u_n)_{n\in \N} \)
Si la série \( \sum u_n \) converge
alors la suite \( (S_n)_{n\in \N} \) converge vers un réel noté \(S\) ( la somme)
Pour tout \(n\in \N^*\),
u_n=S_n-S_{n-1}
Donc ,
\lim_{n }u_n=S-S=0
La réciproque est fausse:
Contre-exemple:
Soit \( (u_n)_{n\in \N^l*} \) définie par: \(u_n=\frac{1}{n}\)
pourtant, \(\sum u_n \) diverge
\lim_n u_n=0
Preuve de la divergence :
Soit \(n\in \N^*\).
Soit \(k \in \N^*\), \( \forall t\in [k,k+1]\) , on a:
\frac{1}{k+1}\leqslant \frac{1}{t} \leqslant \frac{1}{k}
\text{donc, }\int_k^{k+1} \frac{1}{k+1}dt \leqslant \int_k^{k+1} \frac{1}{t}dt \leqslant \int_k^{k+1} \frac{1}{k} dt
\iff \frac{1}{k+1} \leqslant \int_k^{k+1} \frac{1}{t}dt \leqslant \frac{1}{k}
\text{donc,} \sum_{k=1}^n \int_k^{k+1} \frac{1}{t}dt \leqslant \sum_{k=1}^n \frac{1}{k}
\iff \int_1^{n+1} \frac{1}{t}dt \leqslant \sum_{k=1}^n \frac{1}{k}
\iff \left[ \ln (t) \right] _1^{n+1} \leqslant \sum_{k=1}^n \frac{1}{k}
\iff \ln(n+1) \leqslant \sum_{k=1}^n \frac{1}{k}
\lim_n \ln(n+1)=+\infty \text{ donc } \lim_n \sum_{k=1}^n u_k =+\infty \text{(série divergente)}
( Intégration sur \([k,k+1]\)
Soit \( (S_n)_{n\in \N} \) la suite des sommes partielles de la suite \( (u_n)_{n\in \N} \)
Soit \( (T_n)_{n\in \N} \) la suite des sommes partielles de la suite \( (v_n)_{n\in \N} \)
\( \sum u_n \) converge donc la suite \( (S_n)_{n\in \N} \) converge vers un complexe noté \(S\) ( la somme)
\( \sum v_n \) converge donc la suite \( (T_n)_{n\in \N} \) converge vers un complexe noté \(T\) ( la somme)
Soit \( (\lambda,\mu)\in \mathbb{K}^2 \)
\lim\limits_{n} \displaystyle\sum_{k=0}^n \lambda u_k+\mu v_k
= \lim\limits_{n} \displaystyle\sum_{k=0}^n \lambda u_k + \lim\limits_{n} \displaystyle\sum_{k=0}^n \mu v_k
= \lim\limits_{n} \lambda S_n+ \lim\limits_{n}\mu T_n
= \lambda S+\mu T
\text{Donc,} \displaystyle\sum (\lambda u_n+\mu v_n ) \text{converge, et de plus }
\displaystyle\sum_{k=0}^{+\infty} (\lambda u_k +\mu v_k )=
\lambda \displaystyle\sum_{k=0}^{+\infty} u_k +
\mu \displaystyle\sum_{k=0}^{+\infty} v_k
- Si \( \sum u_n \) converge alors la suite \( (S_n)_{n\in \N} \) converge vers un complexe noté \(S\)
Soit \( (S_n)_{n\in \N} \) la suite des sommes partielles de la suite \( (u_n)_{n\in \N} \)
Ainsi, \( \sum \bar{u_n} \) converge car la suite \( (\bar{S_n})_{n\in \N} \) converge vers \(\bar{S}\)
En effet, \( \vert \overline{Sn}-\bar{S} \vert\)=\( \vert \overline{Sn-S} \vert\)= \( \vert Sn-S \vert\) \(\underset{n\to +\infty}{\to} 0\)
Im(u_n)=\frac{u_n-\overline{u_n}}{2i}
\( \sum u_n \) et \( \sum \overline{u_n} \) convergent
donc toute série ayant un terme général qui est une combinaison linéaire de \( u_n \) et \( \bar{u_n} \)
Re(u_n)=\frac{u_n+\overline{u_n}}{2}
Donc :
\sum Re(u_n) \text{ et } \sum Im(u_n) \text{ convergent }
- Réciproquement, si \( \sum Re(u_n) \) et \( \sum Im(u_n) \) convergent.
Etant donné que :
u_n=Re(u_n)+i Im(u_n) \text{( Combinaison linéaire )}
On a :
\sum u_n \text{ converge }
\displaystyle\sum_{k=0}^{+\infty} (Re( u_k) + i~ Im(u_k) )=
\displaystyle\sum_{k=0}^{+\infty} Re(u_k) +~
i \displaystyle\sum_{k=0}^{+\infty} Im(u_k)
Dans ce cas:
Soit \( (S_n)_{n\in \N} \) la suite des sommes partielles de la suite \( (u_n)_{n\in \N} \)
On a donc les équivalences suivantes :
\sum u_n \text{ converge}
\iff (S_n)_n \text{ converge}
\iff (S_n)_n \text{ est majorée}
\( (S_n)_{n\in \N} \) t une suite croissante
Soit \( (S_n)_{n\in \N} \) la suite des sommes partielles de la suite \( (u_n)_{n\in \N} \)
Soit \( (T_n)_{n\in \N} \) la suite des sommes partielles de la suite \( (v_n)_{n\in \N} \)
Ces suites partielles sont croissantes car les termes généraux sont positifs
\sum v_n \text{ converge } \Rightarrow (T_n)_n \text{ est convergente } \Rightarrow (T_n)_n \text{ est majorée par sa somme } T
\forall n\geqslant k_0,
S_n=\sum_{k=0}^{k_0} u_k +\sum_{k=k_0+1}^{n} u_k
\leqslant
\sum_{k=0}^{k_0} u_k +\sum_{k=k_0+1}^{n} v_k
\leqslant \sum_{k=0}^{k_0} u_k +T
(S_n)_n \text{ est majorée } \Rightarrow (S_n)_n \text{ est convergente } \Rightarrow
\sum u_n \text{ converge }
\sum u_n \text{ diverge } \Rightarrow (S_n)_n \text{ est croissante et non majorée } \\\Rightarrow \lim_{n} S_n=+\infty
\forall n\geqslant k_0,
T_n=\sum_{k=0}^{k_0} v_k +\sum_{k=k_0+1}^{n} v_k
\geqslant
\sum_{k=k_0+1}^{n} u_k
\Rightarrow
\sum v_n \text{ diverge }
\forall n\geqslant k_0,
T_n
\geqslant
S_n -\sum_{k=0}^{k_0} u_k
\text{Donc } \lim_{n} T_n=+\infty
\sum\frac{1}{\sqrt{k}} \text{ diverge}
Autre exemple
\forall n \geqslant 1 , \frac{1}{\sqrt{n}} \geqslant \frac{1}{n}
\text{ et , }\sum\frac{1}{n} \text{ diverge}
Vocabulaire : série harmonique
u_n\sim v_n \iff u_n=v_n\varepsilon_n \text{ où } \lim\limits_n \varepsilon_n=1
Il existe un rang \(k_0\in\N\) tel que:
\forall k\geqslant k_0,
1-\frac{1}{2}\leqslant \varepsilon_\leqslant 1+\frac{1}{2}
Donc:
\forall k\geqslant k_0,
\frac{1}{2}v_k\leqslant \varepsilon_k v_k\leqslant \frac{3}{2}v_k
Et pour tout \( n\geqslant k_0\) :
\sum_{k=k_0+1}^n\frac{1}{2}v_k\leqslant
\sum_{k=k_0+1}^n \varepsilon_k v_k\leqslant
\sum_{k=k_0+1}^n \frac{3}{2}v_k
\iff
\frac{1}{2}(T_n-T_{k_0})
\leqslant
S_n-S_{k_0}
\leqslant
\frac{3}{2}(T_n-T_{k_0})
On obtient :
Pour tout \( n\geqslant k_0\) :
\sum u_n \text{ converge}
\iff
\sum v_n \text{ converge}
\frac{1}{2}(T_n-T_{k_0})+S_{k_0}
\leqslant
S_n
\leqslant
\frac{3}{2}(T_n-T_{k_0})+S_{k_0}
- Si \(\sum v_n\) converge alors \( (T_n)_n\) est majorée alors \( (S_n)_n\) est majorée et donc \(\sum u_n\) converge
- Si \(\sum u_n\) converge alors \( (S_n)_n\) est majorée alors \( (T_n)_n\) est majorée et donc \(\sum v_n\) converge
\frac{2}{3}(S_n-S_{k_0})+T_{k_0}
\leqslant
T_n
\leqslant
2(S_n-S_{k_0})+T_{k_0}
Soit \(n\in \N^*\).
Soit \(k \in \N^*\), \( \forall t\in [k,k+1]\) , on a:
\text{donc, }\int_k^{k+1} f(k+1) dt \leqslant \int_k^{k+1} f(t) dt \leqslant \int_k^{k+1} f(k) dt
f(k+1)\leqslant f(t)\leqslant f(k)
( décroissance de \(f\) sur \(R_+^*\) )
( la continuité de \(f\) assure qu'elle est intégrable sur tout segment de \(f\) sur \(R_+^*\) )
\text{donc, }\int_k^{k+1} f(k+1) dt \leqslant \int_k^{k+1} f(t) dt \leqslant \int_k^{k+1} f(k) dt
\text{Ainsi, } \sum_{k=1}^n f(k+1) \leqslant \sum_{k=1}^n \int_k^{k+1} f(t) dt \leqslant \sum_{k=1}^n f(k)
\text{et, } f(k+1) \leqslant \int_k^{k+1} f(t) dt \leqslant f(k)
\iff \sum_{k=2}^{n+1} f(k) \leqslant \int_1^{n+1} f(t) dt \leqslant \sum_{k=1}^n f(k)
Soit \(n\in \N^*\).
\iff \sum_{k=2}^{n+1} f(k) \leqslant \int_1^{n+1} f(t) dt \leqslant \sum_{k=1}^n f(k)
Soit \((S_n)_n\) sommes partielles de \( (f(n))_n\)
Soit \((I_n)_n\) suite définie sur \(\N \) par :\(I_n=\displaystyle\int_0^n f(t)dt \)
S_{n+1}-S_1 \leqslant I_{n+1} -I_1\leqslant S_n-S_0
(S_n)_n \text{ converge}
\iff
(I_n)_n \text{ converge}
Remarque : on peut remplacer 0 par n'importe quel nombre positif et le théorème reste vrai
\sum \frac{1}{n^{\alpha}} \text{ converge}
\(t\mapsto \dfrac{1}{t^{\alpha}}\) est continue ,décroissante et positive sur \([1;+\infty[\)
\iff
\left( \frac{1}{(1-\alpha)n^{\alpha-1}} -\dfrac{1}{1-\alpha}\right)_n \text{ converge}
\iff \alpha-1>0
\iff \alpha >1
\iff
\left(\int_1^n \frac{dt}{t^{\alpha}}\right)_n \text{ converge}
\sum \frac{1}{n^{\alpha}} \text{ converge}
\iff \alpha >1
\displaystyle\int_1^n \dfrac{dt}{t^{\alpha}}
=
\left\{
\begin{array}{l}
\frac{1}{1-\alpha} n^{1-\alpha} -\frac{1}{1-\alpha} & \text{si }\alpha<1\\\\
\ln(n) & \text{si }\alpha=1\\\\
\frac{1}{(1-\alpha)n^{\alpha-1}} -\frac{1}{1-\alpha} & \text{si }\alpha>1
\end{array}
\right.
\iff\left(\int_1^n \frac{dt}{t^{\alpha}}\right)_n \text{ converge}
\displaystyle\int_1^n \dfrac{dt}{t^{\alpha}}
\underset{n\to\infty}{\to}
\left\{
\begin{array}{l}
+\infty & \text{si }\alpha<1\\\\
+\infty & \text{si }\alpha=1\\\\
-\frac{1}{1-\alpha} & \text{si }\alpha>1
\end{array}
\right.
\text { Si } \alpha>1 \text { et } \lim _{k \rightarrow+\infty} k^\alpha u_k=0 \text {, alors }
\exists N_0 \in \N, \forall n\geqslant N_0, 0 \leqslant n^\alpha u_n \leqslant 1
\forall n\geqslant n_0, 0 \leqslant u_n \leqslant \dfrac{1}{n^\alpha}
\( \alpha>1,\text{ donc }\sum \dfrac{1}{n^\alpha}\) est une serie de Riemann convergente.
\text { Si } 0<\alpha \leqslant 1 \text { et } \lim _{k \rightarrow+\infty} k^\alpha u_k=+\infty \text {, alors }
\exists N_0 \in \N, \forall n\geqslant N_0, n^\alpha u_n \geqslant 1
\forall n\geqslant n_0, u_n \geqslant \dfrac{1}{n^\alpha}
\( \alpha\leqslant 1,\text{ donc }\sum \dfrac{1}{n^\alpha}\) est une serie de Riemann divergente.
D'après le théorème des comparaison des séries positives
\(\sum u_n \) converge
\(\sum u_n \) diverge
\sum_{k=0}^n q^k=\dfrac{1-q^{n+1}}{1-q}
\text{Si } 0 < q < 1 :
\text{Si } q=1 :
\text{Si } q > 1 :
=\dfrac{1-e^{(n+1)\ln(q)}}{1-q}
\sum_{k=0}^n q^k=n+1
\sum_{k=0}^n q^k=\dfrac{1-q^{n+1}}{1-q}
=\dfrac{1-e^{(n+1)\ln(q)}}{1-q} \underset{n\to +\infty}{\to}+\infty
\sum q^n \text{ converge et }
\sum_{k=0}^{+\infty} q^k=\dfrac{1}{1-q}
\sum q^n \text{ diverge }
\sum q^n \text{ diverge }
\underset{n\to +\infty}{\to}+\infty
\text{Si } \ell \in \R, \text{ on a nécessairement :} \ell\geqslant 0
\exists N_0 \in \N, \forall n\geqslant N_0, \ell-\varepsilon \leqslant \dfrac{u_{n+1}}{u_n} \leqslant \ell+\varepsilon
\forall \varepsilon>0,
\text{on choisit } \varepsilon \text{ tel que : } \ell<\ell+\varepsilon <1
\text{. (Par exemple } \varepsilon=\frac{1-\ell}{2}
\text{) }
\forall k\geqslant N_0, 0 < \dfrac{u_{k+1}}{u_k} \leqslant \ell+\varepsilon
\text{Ainsi }
\text{Et }
\forall n\geqslant N_0, 0 < \prod_{k=N_0}^n\dfrac{u_{k+1}}{u_k} \leqslant \prod_{k=N_0}^n (\ell+\varepsilon)
\iff \forall n\geqslant N_0, 0 < \dfrac{u_{n+1}}{u_{N_0}} \leqslant (\ell+\varepsilon)^{n-N_0+1}
\iff \forall n\geqslant N_0, 0 < u_{n+1} \leqslant C q^{n}
\iff \forall n\geqslant N_0, 0 < u_{n+1} \leqslant u_{N_0} (\ell+\varepsilon)^{n-N_0+1}
\text{où }\\
q=\ell+\varepsilon\\
C=u_{N_0} (\ell+\varepsilon)^{-N_0+1}
\bullet \text{Si } \ell<1,
<1
\text{Si } \ell \in \R, \text{ on a nécessairement :} \ell\geqslant 0
\exists N_0 \in \N, \forall n\geqslant N_0, \ell-\varepsilon \leqslant \dfrac{u_{n+1}}{u_n} \leqslant \ell+\varepsilon
\forall \varepsilon>0,
\forall n\geqslant N_0, 0 < u_{n+1} \leqslant C q^{n}
\text{avec }\\
q=\ell+\varepsilon
\bullet \text{Si } \ell<1,
- \(q\in[0;1[ \) donc \(\sum q^n\) est une série géométrique convergente
D'après le théorème des comparaison des séries positives
\(\sum u_n \) converge
\text{Si } \ell \in \R, \text{ on a nécessairement :} \ell\geqslant 0
\exists N_0 \in \N, \forall n\geqslant N_0, \ell-\varepsilon \leqslant \dfrac{u_{n+1}}{u_n} \leqslant \ell+\varepsilon
\forall \varepsilon>0,
\bullet \text{Si } \ell>1,
\text{on choisit } \varepsilon \text{ tel que : } 1<\ell-\varepsilon <\ell
\text{. (Par exemple } \varepsilon=\frac{\ell-1}{2}
\text{) }
\forall k\geqslant N_0, \dfrac{u_{k+1}}{u_k} \geqslant \ell-\varepsilon
\text{Ainsi }
>1
\text{Et }
\forall n\geqslant N_0, \prod_{k=N_0}^n\dfrac{u_{k+1}}{u_k} \geqslant \prod_{k=N_0}^n (\ell-\varepsilon)
\iff \forall n\geqslant N_0, \dfrac{u_{n+1}}{u_{N_0}} \geqslant (\ell-\varepsilon)^{n-N_0+1}
\iff \forall n\geqslant N_0, u_{n+1} \geqslant C q^{n}
\iff \forall n\geqslant N_0, u_{n+1} \geqslant u_{N_0} (\ell-\varepsilon)^{n-N_0+1}
\text{où }\\
q=\ell-\varepsilon\\
C=u_{N_0} (\ell-\varepsilon)^{-N_0+1}
\text{Si } \ell \in \R, \text{ on a nécessairement :} \ell\geqslant 0
\exists N_0 \in \N, \forall n\geqslant N_0, \ell-\varepsilon \leqslant \dfrac{u_{n+1}}{u_n} \leqslant \ell+\varepsilon
\forall \varepsilon>0,
\text{avec }\\
q=\ell-\varepsilon
\bullet \text{Si } \ell>1,
- \(q>1 \) donc \(\sum q^n\) est une série géométrique divergente
D'après le théorème des comparaison des séries positives
\(\sum u_n \) diverge
\forall n\geqslant N_0, u_{n+1} \geqslant C q^{n}
\text{Si } \ell=+\infty
\exists N_0 \in \N, \forall n\geqslant N_0, \dfrac{u_{n+1}}{u_n} \geqslant 10
\text{avec }\\
C=u_{N_0}10^{-N_0+1}
- \(\sum 10^n\) est une série géométrique divergente
D'après le théorème des comparaison des séries positives
\(\sum u_n \) diverge
\forall n\geqslant N_0, \prod_{k=N_0}^n\dfrac{u_{k+1}}{u_k} \geqslant \prod_{k=N_0}^n 10
\iff \forall n\geqslant N_0, \dfrac{u_{n+1}}{u_{N_0}} \geqslant 10^{n-N_0+1}
\iff \forall n\geqslant N_0, u_{n+1} \geqslant C 10^{n}
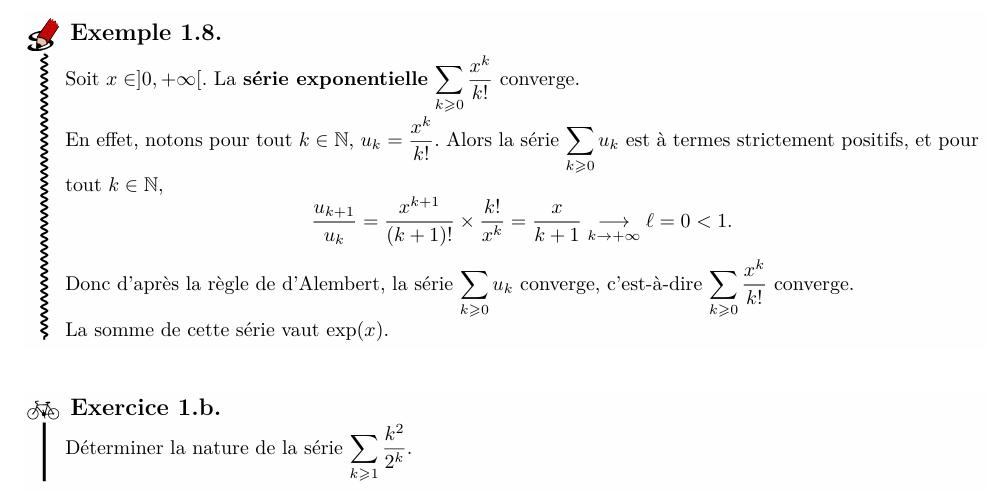
SERIES NUMERIQUES _DEMONSTRATIONS
By intermaths.info
